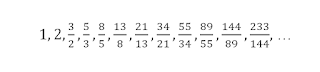Διαστήματα πραγματικών αριθμών...

Ανοιχτό ή κλειστό;

 

Από το σχολικό βιβλίο της Άλγεβρας Α΄ Λυκείου

"Μαθηματικά στο στοιχειωμένο σπίτι"

Κάθε πόρτα στο στοιχειωμένο σπίτι κρύβει κι από ένα μυστήριο, έναν μαθηματικό γρίφο που μπορεί να λυθεί εύκολα με τις απλές εξισώσεις της άλγεβρας.

Τα "Μαθηματικά στο στοιχειωμένο σπίτι" θα βοηθήσουν τους μαθητές να χτίσουν μια βάση στα μαθηματικά, αλλά και να ξεδιαλύνουν τις βασικές έννοιες της άλγεβρας, όπως είναι η ισότητα, η εξίσωση, η μεταβλητή και ο άγνωστος.

Ένα βιβλίο γεμάτο... ανατριχιαστικές εκπλήξεις και διασκεδαστικά παιχνίδια άλγεβρας από τον καταξιωμένο εκπαιδευτικό David A. Adler και τις εκδόσεις Κλειδάριθμος. Είναι κατάλληλο για παιδιά ηλικιών 8 ετών και άνω, ανάλογα πάντα με τη γνωστική ανάπτυξη και τα ενδιαφέροντα του κάθε παιδιού. 

Ο David A. Adler έχει συγγράψει περισσότερα από 300 παιδικά βιβλία, ενώ πριν γίνει συγγραφέας παιδικών βιβλίων, υπήρξε δάσκαλος μαθηματικών στις Ηνωμένες Πολιτείες Αμερικής.

Η τελευταία διάλεξη του Gilbert Strang

Στις προπτυχιακές τους σπουδές, όχι μόνο στο Μαθηματικό, αλλά και σε πάρα πολλά τμήματα θετικών επιστημών ή μηχανικών, οι φοιτητές διδάσκονται το μάθημα της Γραμμικής Άλγεβρας.

Ο Gilbert Strang (γεν. 1934) δίδαξε Γραμμική Άλγεβρα για 61 χρόνια και εκατομμύρια άνθρωποι στον κόσμο έμαθαν από αυτόν τον σπουδαίο καθηγητή, είτε μέσω των όμορφων διαλέξεών του, ή μελετώντας τα βιβλία του. Οι βιντεοσκοπημένες διαλέξεις του είναι πολύ δημοφιλείς στο YouTube και το κανάλι MIT OpenCourseWare. Αυτή είναι η τελευταία διάλεξη που δίνει (Μάιος 2023), στο MIT της Μασαχουσέτης, σε ηλικία 88(!) ετών.

Το βιβλίο του Gilbert Strang "Γραμμική Άλγεβρα και εφαρμογές", σε μετάφραση Π. Πάμφιλου από τις Πανεπιστημιακές Εκδόσεις Κρήτης

Μπορείτε να παρακολουθήσετε μια πλήρη playlist διαλέξεων του Gilbert Strang πάνω σε όλη σχεδόν τη Γραμμική Άλγεβρα εδώ... 

 

Καλό Πάσχα!

Πηγή εικόνας

Το φετινό Πάσχα ας είναι μια ευκαιρία να κοιτάξουμε μπροστά με ελπίδα και γύρω μας με αγάπη! 

Καλό Πάσχα σε όλους και Καλή Ανάσταση! 

Γρίφος: Φυσική τριάδα

 

Κάποιος υποστηρίζει ότι γνωρίζει τρεις φυσικούς αριθμούς x, y και z

που ικανοποιούν την εξίσωση

28x + 30y + 31z = 365.

Έχει δίκιο;;;

Πηγή γρίφου:

ΜΑΘΗΜΑΤΙΚΟΙ ΓΡΙΦΟΙ 1 - 150 προβλήματα από τη στήλη "Σπαζοκεφαλιές" του περιοδικού Quantum, εκδόσεις "Κάτοπτρο", 1999

Προσεταιριστική ιδιότητα: Πόσο προφανής είναι;

Είναι προφανές ότι ισχύει

63 + 48 = 27 + 84 ;

Πρόκειται για μια ορθή μαθηματική πρόταση, χωρίς ενδιαφέρον, που επαληθεύεται σε δευτερόλεπτα. Είναι όμως προφανής; Αν "προφανής" σημαίνει ότι ο λόγος για τον οποίο ισχύει είναι σαφώς κατανοητός, χωρίς ανάγκη επαλήθευσης, τότε οι περισσότεροι θα απαντούσαν αρνητικά.

Είναι, τώρα, προφανές ότι

(27 + 36) + 48 = 27 + (36 + 48) ;

Ασφαλώς, για την πλειοψηφία: η ενστικτώδης (και ορθή) αντίδραση είναι ότι ο τρόπος με τον οποίο "συμμαζεύουμε" τους όρους ενός αθροίσματος δεν μπορεί να επηρεάσει το αποτέλεσμα. Ο έγκυρος μαθηματικός όρος για το συμμάζεμα αυτό και την τοποθέτηση των αριθμών σε "παρέες" είναι "προσεταιρίζουμε" και η ενστικτώδης αντίδραση είναι η αποδοχή της προσεταιριστικής ιδιότητας της πρόσθεσης για πραγματικούς αριθμούς:

Την προσεταιριστική ιδιότητα διαθέτει και η πράξη του πολλαπλασιασμού στους πραγματικούς αριθμούς:

Εκτός, όμως, από το σύνολο των πραγματικών αριθμών εφοδιασμένο με τις πράξεις τις πρόσθεσης και του πολλαπλασιασμού, οι μαθηματικοί ενδιαφέρθηκαν να ορίσουν και άλλα σύνολα, πιο αφηρημένα, για πολλούς και διάφορους σκοπούς. Η Γραμμική Άλγεβρα ασχολείται με διάφορα είδη πράξεων (όπως η πρόσθεση ή ο πολλαπλασιασμός) για διάφορα είδη αντικειμένων (όχι αναγκαστικά πραγματικούς αριθμούς). Μας ενδιαφέρει αν η πράξη με την οποία έχει εφοδιαστεί ένα σύνολο είναι, μεταξύ άλλων, προσεταιριστική. 

Προσεταιριστική πράξη

Μια διμελής πράξη ✱ σ' ένα σύνολο S λέγεται προσεταιριστική, αν (α ✱ β) ✱ γ = α ✱ (β ✱ γ), για κάθε α, β, γ ∈ S.

Είναι άδικο να παραβλέψουμε την προσεταιριστική ιδιότητα ως κάτι τετριμμένο. Η προσεταιριστικότητα της πράξης μπορεί να μην ισχύει πάντα, αλλά, ακόμη κι αν ισχύει, δεν είναι και τόσο προφανής. Στον κόσμο της Γραμμικής Άλγεβρας, αν και οι μη προσεταιριστικές πράξεις είναι σπάνιες, πράξεις για τις οποίες η προσεταιριστικότητα δεν είναι αυτονόητη, συναντώνται συχνότερα.

Κουίζ:

1. Ορίζουμε μια νέα πρόσθεση στους πραγματικούς αριθμούς, συμβολιζόμενη ως ⊕, όπου:

α⊕β = 2α + 2β

Είναι η ⊕ προσεταιριστική;

Σχόλιο: Το + στο δεύτερο μέλος σημαίνει τη συνήθη πρόσθεση.

2. Στο σύνολο {0, 1, 2} που αποτελείται από τρία στοιχεία, ορίζουμε έναν νέο πολλαπλασιασμό, που τον συμβολίζουμε με ⊗. Στον παρακάτω πίνακα πολλαπλασιασμού βλέπουμε πώς ορίζεται ο πολλαπλασιασμός ⊗:

⊗	0	1	2
0	0	0	0
1	0	1	2
2	0	2	1

Είναι η ⊗ προσεταιριστική;

Σχόλιο: Η πράξη αυτή καλείται στη Γραμμική Άλγεβρα "πολλαπλασιασμός modulo 3" (mod3, μοδίω 3), ενώ το σύνολο {0, 1, 2} καλείται "οι ακέραιοι modulo 3" και συμβολίζεται ως  ℤ3 .

Πηγές:

John B. Fraleigh (2003, 4η έκδοση). Εισαγωγή στην Άλγεβρα (μετ. Γιαννόπουλος). Πανεπιστημιακές Εκδόσεις Κρήτης, Ηράκλειο (Το πρωτότυπο έργο δημοσιεύθηκε το 1967).

Paul Halmos (2012). Προβλήματα Γραμμικής Άλγεβρας (μετ. Τουμάσης & Γραμματίκας). Ευρύαλος Απόλλων, Τρίκαλα (Το πρωτότυπο έργο δημοσιεύθηκε το 1995).

Αυτό που δεν πέτυχε ο μαρξισμός, το πέτυχε η Άλγεβρα!

Η Άλγεβρα με τη Θεωρία Ομάδων κατάφερε ό,τι δεν έχει καταφέρει ο... μαρξισμός: Την εξίσωση των τάξεων (ή κλάσεων)!

Φωτογραφία από τις σημειώσεις που κρατούσα στο μεταπτυχιακό μάθημα "Άλγεβρα Ι" με καθηγητή τον Ν.Μαρμαρίδη, 2014

Διαβάστε για την εξίσωση των τάξεων (ή κλάσεων) εδώ...

Γρίφος: Οι μυστηριώδεις πράξεις

Στην Άλγεβρα, μπορούμε με ένα οποιοδήποτε σύμβολο να συμβολίσουμε μια πράξη ή μια σειρά πράξεων που ορίσαμε μεταξύ δύο αριθμών. Αρκεί η πράξη αυτή να είναι καλά ορισμένη, δηλαδή το αποτέλεσμα της πράξης μεταξύ των δύο αριθμών να ορίζεται μονοσήμαντα και να ανήκει στο ίδιο σύνολο αριθμών με τους δύο αρχικούς.

Βρείτε ποια ή ποιες πράξεις ορίζονται με το σύμβολο ⨀ κι έπειτα βρείτε τον αριθμό στη θέση του ερωτηματικού.

Μαγικά ή μαθηματικά;

Ένας καθηγητής Μαθηματικών είπε στους μαθητές του:

• Σκεφτείτε έναν αριθμό.
• Τώρα διπλασιάστε τον.
• Στο αποτέλεσμα, να προσθέσετε τον αριθμό 10.
• Το άθροισμα που βρήκατε να το διαιρέσετε με το 2.
• Από το πηλίκο, να αφαιρέσετε τον αριθμό που σκεφτήκατε αρχικά.

Κάθε μαθητής πρέπει να έχει βρει αποτέλεσμα τον αριθμό 5, ανεξάρτητα από ποιον αριθμό σκέφτηκε αρχικά.

Ο μαθηματικός δεν διάβαζε το μυαλό των μαθητών του... Πώς εξηγείται όμως το ότι ήξερε το τελικό αποτέλεσμα;

Έστω ότι x είναι ο αριθμός που σκέφτηκε κάποιος μαθητής. 

Τότε, αν τον διπλασιάσει γίνεται 2x. 

Στο αποτέλεσμα προσθέτει το 10 και προκύπτει το 2x + 10. 

Τον αριθμό που βρίσκει τον διαιρεί με το 2, οπότε βρίσκει (2x + 10):2. 

Αφαιρεί τον αριθμό που σκέφτηκε αρχικά και βρίσκει αποτέλεσμα (2x + 10):2 - x. 

O μαθηματικός ισχυρίζεται ότι το αποτέλεσμα πρέπει να είναι ίσο με 5, οπότε προκύπτει η εξίσωση:

(2x + 10):2 - x = 5 ⇔

2x + 10 - 2x = 10 ⇔

2x - 2x = 10 - 10 ⇔

0x = 0

H εξίσωση είναι ταυτότητα, άρα επαληθεύεται για κάθε αριθμό που μπορεί να σκέφτηκαν οι μαθητές.

Δεν είναι μαγικά... είναι απλά μαθηματικά!

Καλή Χρονιά!

Καλή και δημιουργική χρονιά σε όλους!!!

Παρακάτω σας έχω κι έναν μαθηματικό γρίφο... για να ξεκινήσει καλά η νέα χρονιά!!! ;)

"Αριθμητική με το νου"

Ο Nikolay Bogdanov-Belsky (1868 - 1945) ήταν Ρώσος ζωγράφος που ακολουθούσε τα ρεύματα του Ρεαλισμού και του Ιμπρεσιονισμού. Πολλά από τα έργα του έχουν ηθογραφικό χαρακτήρα και αποτελούνται από πορτρέτα, ιμπρεσιονιστικά τοπία και απεικονίσεις της καθημερινής ζωής, με κύριο στοιχείο τα παιδιά και την εκπαίδευση τους.

To 1895, o Nikolay Bogdanov-Belsky ζωγράφισε τον πίνακα «Αριθμητική με το νου. Στο δημόσιο σχολείο του S. Rachinsky», ή κατ' άλλους, «Ένα δυσνόητο πρόβλημα». Ο δάσκαλος που απεικονίζεται είναι ο S. Rachinsky, καθηγητής φυσικής, ο οποίος εγκατέλειψε το πανεπιστήμιο για να υπηρετήσει ως απλός δάσκαλος σε κάποιο χωριό.

Οι περισσότεροι, όμως, όταν θαυμάζουν το έργο τέχνης, παραβλέπουν το πρόβλημα που είναι γραμμένο στον πίνακα της τάξης... Το πρόβλημα ζητάει τον υπολογισμό της αριθμητικής παράστασης:

(10²+11²+12²+13²+14²)/365

Μπορείτε να κάνετε τον υπολογισμό με το μυαλό σας;

Πηγές:

Yakov Perelman, Διασκεδαστικά Μαθηματικά, Εκδόσεις Κάτοπτρο, 2001

https://twitter.com/fermatslibrary

Γραμμικό σύστημα 2x2 και η απάντηση ενός μαθητή...

Βρες το ζεύγος των αριθμών x και y που επαληθεύει το παραπάνω σύστημα.

1/6/2018: Παγκόσμια ημέρα του χρυσού αριθμού «φ»... (Μέρος 1º - Γνωριμία με τον αριθμό «φ»)

Τι κοινό έχουν οι ζωγραφικοί πίνακες της Αναγέννησης, το κουνουπίδι, η αναπαραγωγή των κουνελιών και μια πιστωτική κάρτα; Η απάντηση είναι ο αριθμός 1,61803398874989484..., ο "χρυσός αριθμός", ή "χρυσή αναλογία". Τα δεκαδικά του ψηφία είναι άπειρα και η ακολουθία τους δεν επαναλαμβάνεται. Μάθετε τι τον καθιστά τόσο μαγικό!

Όπως ο π (3,14) εκφράζει το πιο τέλειο γεωμετρικό σχήμα, τη σφαίρα, έτσι και ο φ (1,618) είναι ο αριθμός της «ομορφιάς». Ο μοναχός του 15^ου αιώνα Luca Pacioli, επηρεασμένος από την αντίληψη της εποχής ότι οι νέες γνώσεις της επιστήμης έπρεπε να ενταχθούν στο εκκλησιαστικό δόγμα, τον ονόμασε «Θεία Αναλογία» («Divina Proportione»). Ο Leonardo DaVinci τον ονόμασε «Χρυσό Αριθμό». Αιώνες αργότερα, ο μαθηματικός Mark Barr θα τον συμβόλιζε με το ελληνικό γράμμα φ, προς τιμήν του γλύπτη Φειδία, ο οποίος ήταν από τους πρώτους που δημιουργούσαν έργα με βάση τον αριθμό αυτό.

ΤΑ ΕΥΘΥΓΡΑΜΜΑ ΤΜΗΜΑΤΑ ΤΟΥ ΕΥΚΛΕΙΔΗ

Η αφετηρία είναι γεωμετρική. Ο Ευκλείδης στα «Στοιχεία» έδωσε τον πρώτο γραπτό ορισμό της χρυσής τομής, την οποία ονόμασε «άκρος και μέσος λόγος».

Ο Ευκλείδης παίρνει ένα ευθύγραμμο τμήμα και το διαιρεί σε δύο τμήματα. Η χρυσή τομή είναι εκείνο το σημείο που χωρίζει το ευθύγραμμο τμήμα στα δυο τμήματα a, b, έτσι ώστε  ο λόγος του αθροίσματος τους a+b προς τη μεγαλύτερη ποσότητα είναι ίσος με το λόγο της μεγαλύτερης ποσότητας προς τη μικρότερη.

Ο λόγος αυτός λέγεται «χρυσός λόγος» και σύμφωνα με τον ορισμό του Ευκλείδη, υπολογίζεται ότι έχει αριθμητική τιμή 1,618..., δηλαδή ότι το μεγαλύτερο τμήμα θα έχει πάντα 1,618... φορές μεγαλύτερο μήκος από το μικρότερο. 

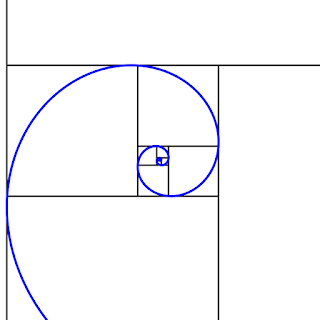
ΧΡΥΣΟ ΟΡΘΟΓΩΝΙΟ ΚΑΙ ΧΡΥΣΗ ΕΛΙΚΑ

Ένα ορθογώνιο παραλληλόγραμμο λέγεται «χρυσό», όταν το πηλίκο της μεγαλύτερης προς τη μικρότερη πλευρά του ισούται με φ. 

Αυτό το ορθογώνιο έχει μια ιδιότητα που το ξεχωρίζει από όλα τα άλλα: αν αφαιρέσουμε από τη μια πλευρά το μεγαλύτερο δυνατό τετράγωνο, απομένει ένα καινούργιο ορθογώνιο, που είναι επίσης χρυσό, και αυτό μπορεί να συνεχιστεί επ’ άπειρον. 

Αν ενώσει κανείς με μια καμπύλη τις κορυφές όλων αυτών των ορθογωνίων, που είναι και χρυσές τομές, σχηματίζεται μια λογαριθμική έλικα, η «χρυσή έλικα».

Αν θέλει κανείς να δει ένα χρυσό ορθογώνιο αρκεί να κοιτάξει μια πιστωτική κάρτα, το σχήμα της οποίας είναι ακριβώς αυτό. 

ΧΡΥΣΟ ΤΡΙΓΩΝΟ

Χρυσό λέγεται κάθε ισοσκελές  τρίγωνο στο οποίο ο λόγος της μεγάλης πλευράς προς τη μικρή θα είναι ίσος με φ. Κάθε ισοσκελές με γωνία κορυφής 36˚ είναι χρυσό.

ΤΟ ΣΥΜΒΟΛΟ ΤΩΝ ΠΥΘΑΓΟΡΕΙΩΝ

Η χρυσή αναλογία ήταν γνωστή στους Πυθαγορείους. Το σύμβολο της αδελφότητας των Πυθαγορείων ήταν το «πεντάγραμμο» ή «πεντάλφα», το αστέρι δηλαδή που σχηματίζεται από τις πέντε διαγωνίους του κανονικού πενταγώνου. Η χρυσή αναλογία εμφανίζεται στις πλευρές του αστεριού. 

Αποδεικνύεται ότι κάθε πλευρά του «πενταγράμμου» διαιρεί τις δύο άλλες σε χρυσή τομή.

Ακόμη, το πηλίκο του εμβαδού του κανονικού πενταγώνου με κορυφές τις άκρες της πεντάλφα προς το εμβαδόν του κανονικού πενταγώνου που σχηματίζεται εντός του αστεριού ισούται με φ.

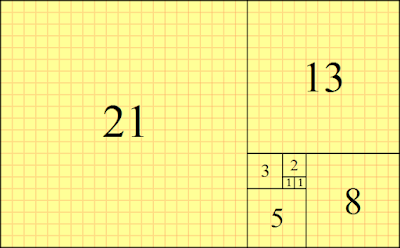
ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΗΣ ΑΝΑΠΑΡΑΓΩΓΗΣ ΤΩΝ ΚΟΥΝΕΛΙΩΝ

Ο Leonardo Pisano Fibonacci (1170-1240) γεννήθηκε στην Πίζα. Ο πατέρας του Leonardo, Guilielmo Bonacci, ήταν γραμματέας της Δημοκρατίας της Πίζας στη Βορειοαφρικανική πόλη Bugia. Ο Fibonacci μεγάλωσε εκεί και η εκπαίδευσή του επηρεάστηκε σημαντικά από τους Μαυριτανούς αλλά και από τα ταξίδια που έκανε αργότερα κατά μήκος της Μεσογειακής ακτής (Αίγυπτο, Συρία, Ελλάδα, Σικελία και Προβηγκία). Έτσι, μελέτησε και έμαθε τις μαθηματικές τεχνικές και τα αριθμητικά συστήματα που είχαν υιοθετηθεί σε εκείνες τις περιοχές.

Γύρω στο 1200, ο Fibonacci επέστρεψε στην Πίζα, όπου για τα επόμενα 25 χρόνια επεξεργαζόταν τις δικές του μαθηματικές συνθέσεις. Στο βιβλίο του με τίτλο "Liber Abaci",  εισήγαγε την έννοια της ακολουθίας στα Μαθηματικά της Δυτικής Ευρώπης. Σ’ έναν περίφημο, πλέον, συλλογισμό, προσπάθησε να υπολογίσει την ταχύτητα αναπαραγωγής των κουνελιών στη γη, κάτω από ιδανικές συνθήκες. Ο Fibonacci υπέθεσε ότι έχουμε 1 ζευγάρι κουνελιών, το οποίο αρχίζει να αναπαράγεται από τον πρώτο μήνα και μετά από κάθε μήνα κύησης, φέρνει στον κόσμο ένα ακόμη ζευγάρι. Κάθε νέο ζευγάρι είναι έτοιμο να τεκνοποιήσει 1 μήνα μετά τη γέννησή του, γεννά 1 μήνα μετά και συνεχίζει να αναπαράγεται με τον ίδιο ρυθμό. Πόσα ζευγάρια κουνελιών θα έχουμε στο τέλος του πρώτου χρόνου;

1. Αρχικά υπάρχει ένα ζευγάρι κουνελιών.
2. Στο τέλος του 1ου μήνα το αρχικό ζευγάρι είναι έτοιμο να ζευγαρώσει, αλλά υπάρχει μόνο αυτό.
3. Στο τέλος του 2ου μήνα έχουμε το αρχικό ζευγάρι και το πρώτο ζευγάρι παιδιών του. Συνολικά 2 ζευγάρια κουνελιών. 
4. Στο τέλος του 3ου μήνα έχουμε το αρχικό ζευγάρι, το πρώτο ζευγάρι παιδιών του, (που είναι έτοιμα κι αυτά να τεκνοποιήσουν) και ένα δεύτερο ζευγάρι παιδιών του. Συνολικά 3 ζευγάρια κουνελιών. 
5. Στο τέλος του 4ου μήνα έχουμε το αρχικό ζευγάρι, το πρώτο ζευγάρι παιδιών και το πρώτο δικό του ζευγάρι παιδιών, το δεύτερο ζευγάρι παιδιών, που είναι έτοιμα να τεκνοποιήσουν, και ένα νέο, τρίτο ζευγάρι παιδιών. Συνολικά 5 ζευγάρια κουνελιών. 

Με βάση αυτή την υπόθεση, ο Fibonacci ανακάλυψε ότι τα ζευγάρια των κουνελιών αυξάνονταν κάθε μήνα σύμφωνα με μια άπειρη ακολουθία αριθμών: 
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 114, 233, 377, 610...

Μπορείτε να εντοπίσετε το μοτίβο που κρύβεται πίσω από αυτή την αλληλουχία; 

Οι αριθμοί αυτοί ονομάστηκαν «αριθμοί Fibonacci» και αποτελούν τη λεγόμενη «Ακολουθία Fibonacci». Εκτός από τους δύο πρώτους αριθμούς που είναι το 1, κάθε αριθμός της ακολουθίας Fibonacci ισούται με το άθροισμα των δύο προηγουμένων: 

α_ν+2 = α_ν+1 + α_ν

Αν και υπάρχουν αναφορές ότι αυτή η ακολουθία είχε αναφερθεί περίπου μισό αιώνα πριν, από τους Ινδούς Gospala και Hemachandra, ο Fibonacci συνάντησε αυτή την ακολουθία μελετώντας την Μεγάλη Πυραμίδα του Χέοπα στην Αίγυπτο, η οποία και είναι χτισμένη με βάση τον αριθμό  φ.

Όμως, τι σχέση έχει η ακολουθία Fibonacci με το χρυσό αριθμό; 

Κατασκευάζουμε μια ακολουθία με τους λόγους των διαδοχικών όρων της ακολουθίας Fibonacci.

Μπορούμε να πάρουμε ένα κομπιουτεράκι και να κάνουμε τις διαιρέσεις. Θα διαπιστώσουμε πως όσο προχωράμε στην ακολουθία, το πηλίκο θα προσεγγίζει όλο και περισσότερο τον αριθμό φ.

π.χ.
5/3=1,66666666...
89/55=1,6181818...
377/233=1,618025751
987/610=1,618032787
46368/28657=1,618033988

Σε μαθηματικούς όρους, αυτό σημαίνει πως η ακολουθία των λόγων δύο διαδοχικών αριθμών Fibonacci έχει ως όριο τον αριθμό φ. Το συμπέρασμα αυτό αποδείχτηκε από τον μαθηματικό Robert Simpson το 1753, δηλαδή πεντέμιση αιώνες αργότερα από τον ορισμό της ακολουθίας από τον Fibonacci!

Εμβαθύνοντας λίγο στην Ανάλυση...

Όπως κάθε ακολουθία που προσδιορίζεται από αναδρομική σχέση, έτσι και η ακολουθία Fibonacci έχει έναν τύπο κλειστής μορφής, δηλαδή έναν γενικό τύπο που δίνει τον ν-οστό όρο. Αυτός είναι γνωστός ως τύπος του Binet:

Υπολογίζεται το όριο της ακολουθίας των λόγων δύο διαδοχικών όρων της F(n):

Παρόμοια, οι αριθμοί Fibonacci προσεγγίζουν εντυπωσιακά και τη χρυσή έλικα. Παρακάτω βλέπουμε μια κάλυψη του επιπέδου με τετράγωνα, οι πλευρές των οποίων είναι διαδοχικοί αριθμοί Fibonacci.

Ενώνουμε κάθε φορά δύο απέναντι κορυφές των τετραγώνων γράφοντας τόξα κύκλων. Σχηματίζεται η έλικα (ή σπείρα) Fibonacci, η οποία αποτελεί προσέγγιση της χρυσής έλικας. 

Η χρυσή αναλογία συνδέεται, δηλαδή, με τον πολλαπλασιασμό των κουνελιών, παρόλο που η Ακολουθία Fibonacci σχηματίστηκε ανεξάρτητα από την ευκλείδεια γεωμετρία. 

Ο φ ΚΑΙ Η ΑΛΓΕΒΡΑ

• Υπολογισμός του φ:

Για να υπολογίσουμε την τιμή του φ, ξεκινάμε από τον ορισμό:

Απλοποιώντας το αριστερό κλάσμα και αντικαθιστώντας το b/a = 1/φ, παίρνουμε

άρα,

Πολλαπλασιάζοντας και τα δύο μέλη με φ, παίρνουμε: φ + 1 = φ²

επομένως προκύπτει η εξίσωση: φ² – φ – 1 = 0

Χρησιμοποιώντας τη μέθοδο επίλυσης εξισώσεων 2^ου βαθμού, με διακρίνουσα, βρίσκουμε:

Επειδή το φ εκφράζει αναλογία μεταξύ θετικών ποσοτήτων, το φ είναι αναγκαστικά θετικό:

• Ιδιότητες:

1) Αν ελαττώσουμε τον φ κατά 1 μονάδα, αντιστρέφεται!

Επειδή φ = 1 + 1/φ , προκύπτει ότι 

2) Αν υψώσουμε τον φ στο τετράγωνο, αυξάνεται κατά 1 μονάδα!

Επειδή φ² = 1 + φ, παίρνουμε 

και αυτό μπορεί να συνεχιστεί επ’ άπειρον.

3) Ακόμα, για τον αριθμό φ ισχύει ότι:

• φ = 1φ
• φ² = 1φ + 1
• φ³ = 2φ + 1
• φ⁴ = 3φ + 2
• φ⁵ = 5φ + 3
• φ⁶ = 8φ + 5 …

Παρατηρούμε, δηλαδή, ότι στις δυνάμεις του φ «κρύβεται» η ακολουθία Fibonacci!

Η παραπάνω έκφραση μπορεί να χρησιμοποιηθεί για την ανάλυση μεγάλων δυνάμεων φⁿ σε έναν γραμμικό συνδυασμό του φ και του 1. Η σχέση που προκύπτει παράγει αριθμούς Fibonacci ως γραμμικούς συντελεστές:

φⁿ =  F(n) φ + F(n-1)

4) Μια άλλη έκφραση του αριθμού φ βασισμένη μόνο στο ψηφίο του 5 είναι η παρακάτω και οφείλεται στον Erol Karazincir:

ΠΑΝΤΑΧΟΥ ΠΑΡΩΝ…

Το Σύμπαν δείχνει να τρέφει μια ιδιαίτερη αδυναμία για τον αριθμό φ με τα άπειρα δεκαδικά ψηφία. 

(Συνεχίζεται...)

Πηγές:

Περιοδικό Focus

goldennumber.net

wikipedia.org
Πανεπιστημιακές σημειώσεις "Ευκλείδεια και μη Ευκλείδειες Γεωμετρίες" καθηγητή Χρ.Μπαϊκούση, 2011

Merry X-mas!

Καλές γιορτές σε όλους!!! Θα σας ευχηθώ μέσα από αυτή την εξίσωση...

Μαγικά ή μαθηματικά;

Είμαστε έτοιμοι να δούμε ένα... μαγικό τρικ (και την απομυθοποίησή του); Ξεκινάμε...

• Σκέψου έναν αριθμό.
• Πρόσθεσε το 7 στον αριθμό που διάλεξες.
• Αφαίρεσε το 2.
• Τώρα αφαίρεσε τον αριθμό που σκέφτηκες αρχικά.
• Πολλαπλασίασε τον αριθμό που προέκυψε με το 3.
• Τέλος, πρόσθεσε το 5.

Ξέρω ότι ο αριθμός που προέκυψε είναι το 20. Έτσι δεν είναι;

Όχι, δεν έχω καμιά ικανότητα να διαβάζω το μυαλό των άλλων... Πίσω από το τρικ κρύβεται απλώς η παρακάτω αλγεβρική παράσταση:

(x+7-2-x)·3+5 = 5·3+5

                        = 15+5

                    = 20

Δεν είναι μαγικά... είναι απλά μαθηματικά!