Τετάρτη 25 Δεκεμβρίου 2019
Δευτέρα 23 Δεκεμβρίου 2019
Δυσαριθμησία: Μέρος 3º - Αποτελεσματική παρέμβαση
Στο πρώτο μέρος αυτής της σειράς άρθρων, περιγράφεται η δυσαριθμησία ως ειδική μαθησιακή δυσκολία και τονίζεται η σημασία της προληπτικής διδασκαλίας. Στο δεύτερο μέρος αναλύονται τα προειδοποιητικά σημάδια σχετικά με την πιθανή ύπαρξη δυσαριθμησίας και δίνονται κάποιες πληροφορίες σχετικά με τη διαδικασία της διάγνωσης. Αυτό είναι το τρίτο και τελευταίο μέρος, όπου θα προσπαθήσω να περιγράψω, χωρίς να γίνω κουραστική, διάφορες μεθόδους παρέμβασης που εφαρμόζονται προκειμένου να καταφέρει ο μαθητής με δυσαριθμησία να υπερβεί τις δυσκολίες του. Πολλές από τις μεθόδους που αναφέρονται, είμαι σίγουρη ότι βοηθάνε όλα τα παιδιά να μάθουν μαθηματικά, είτε έχουν μαθησιακές δυσκολίες είτε όχι.
Αποτελεσματική παρέμβαση
Μετά την οικεία διάγνωση, πρέπει να παρέχεται στο παιδί με δυσαριθμησία ένα πρόγραμμα παρέμβασης ειδικά σχεδιασμένο για αυτό. Επειδή το παρόν τυπικό εκπαιδευτικό σύστημα δεν είναι συμβατό με τον τρόπο με τον οποίο μαθαίνουν τα παιδιά με δυσαριθμησία, χρειάζεται εξατομικευμένη μεταχείριση από ειδικό, φιλική προς το μαθησιακό στυλ του παιδιού. Αξίζει να τονιστεί ότι η δυσαριθμησία δεν είναι ένα πρόβλημα ή μια πάθηση ώστε να ψάχνουμε θεραπεία. Δεν περιμένουμε η δυσαριθμησία να "φύγει", αλλά βοηθάμε το παιδί να συμφιλιωθεί μαζί της, του διδάσκουμε τρόπους να την υπερβεί και να αναπτύξει τους δικούς του μηχανισμούς ώστε να κάνει σωστά τις μαθηματικές πράξεις και να επιλύει προβλήματα μαθηματικής φύσεως.
Μέσα από το εξατομικευμένο πρόγραμμα παρέμβασης:
- Γίνεται αγωγή προσανατολισμού. Μόλις οι μαθητές βεβαιωθούν μέσω του προσανατολισμού ότι η αντίληψή τους είναι σωστή, θα είναι σε θέση να υπερβαίνουν τις αριθμητικές τους δυσκολίες με μη παραδοσιακές μεθόδους, οι οποίες θα βασίζονται στις οπτικοχωρικές τους δεξιότητες, στη φαντασία τους και στη δημιουργικότητά τους.
- Αξιοποιείται η πολυαισθητηριακή μέθοδος διδασκαλίας, σύμφωνα με την οποία το παιδί πρέπει να δει, να ακούσει και να αισθανθεί έναν αριθμό.
- Διδάσκονται οι τέσσερις βασικές πράξεις με χρήση αντικειμένων, όπως μεζούρα, κέρματα, τραπουλόχαρτα, ξυλομπογιές, πλαστελίνη κλπ. βάση του οπτικού και του κιναισθητικού στυλ μάθησης που έχουν πολλά παιδιά.
- Πραγματοποιείται ουσιαστική εκμάθηση της προπαίδειας με μη συμβατικούς τρόπους.
- Επιλύονται τα μαθηματικά προβλήματα αφού πρώτα οπτικοποιηθούν σε μια εικόνα ή ένα σχήμα.
- Τονώνεται η αυτοπεποίθηση του παιδιού μέσα από διαρκείς επιβραβεύσεις των προσπαθειών του.
- Γίνεται διδασκαλία των Μαθηματικών μέσα από εφαρμογές στη σύγχρονη καθημερινότητα (ίντερνετ, βιντεοπαιχνίδια, GPS κλπ) και με χρήση των Νέων Τεχνολογιών.
- Μέσα από το παιχνίδι, μπορούμε πολύ συχνά να πάρουμε αφορμή για τη διδασκαλία μιας μαθηματικής έννοιας.
Αυτή η εξατομίκευση της διδασκαλίας, η καθημερινή εξάσκηση και οι στοχευμένες διδακτικές εμπειρίες εφοδιάζουν το παιδί με τα κατάλληλα εργαλεία που το βοηθούν να μάθει να χειρίζεται σωστά τους αριθμούς με τον δικό του, μοναδικό τρόπο.
"Κάθε παιδί μπορεί να μάθει και να αγαπήσει τα μαθηματικά, αρκεί να τα διδαχτεί με τον τρόπο που του ταιριάζει,αξιοποιώντας τα δυνατά του σημεία".(Ιωάννης Καραγιαννάκης)
Βιβλιογραφία
Αγαλιώτης, Ι. (2000). Μαθησιακές Δυσκολίες στα Μαθηματικά. Αιτιολογία, αξιολόγηση, αντιμετώπιση. Αθήνα: Ελληνικά Γράμματα.
Hannel, G. (2013) (2nd edition). Dyscalculia: Action plans for successful learning in Mathematics. New York: Routledge.
Karagiannakis, G., & Baccaglini-Frank, A. (2014). The De-Di-Ma battery: A tool for identifying students' mathematical learning profiles. Health Psychology Review, 2(4), 291-297.
Rousselle, L., & Noel. M. P. (2007). Basic numerical skills in children with mathematics learning disabilities: A comparison of symbolic vs non-symbolic number magnitude processing. Cognition, 102(3), 361-395.
Στασινός, Δ. (2003) (Επιμ). Μαθησιακές δυσκολίες του παιδιού και του εφήβου. Η εμπειρία της σύγχρονης Ευρώπης. Αθήνα: Gutenberg.
Shams. L. & Seitz, A. R. (2008). Benefits of Multisensory Learning. Trends in Cognitive Sciences, 12(11), 411-417.
Wilson, A. J., & Dehaene, S. (2007). Number sense and developmental dyscalculia. Human behavior, learning and the developing brain: Atypical development, 2, 212-237.
Σημειώσεις από τα βιωματικά σεμινάρια του δρ. Καραγιαννάκη Ιωάννη: "Δυσαριθμησία: Στρατηγικές αντιμετώπισης των μαθησιακών δυσκολιών στα Μαθηματικά μαθητών πρωτοβάθμιας και δευτεροβάθμιας εκπαίδευσης" (17/10/2015) & "Αντιμετώπιση των δυσκολιών στα Μαθηματικά με έξυπνο τρόπο" (20/05/2017), Διεπιστημονικό Κέντρο Ηπείρου, Ιωάννινα.
Hannel, G. (2013) (2nd edition). Dyscalculia: Action plans for successful learning in Mathematics. New York: Routledge.
Karagiannakis, G., & Baccaglini-Frank, A. (2014). The De-Di-Ma battery: A tool for identifying students' mathematical learning profiles. Health Psychology Review, 2(4), 291-297.
Rousselle, L., & Noel. M. P. (2007). Basic numerical skills in children with mathematics learning disabilities: A comparison of symbolic vs non-symbolic number magnitude processing. Cognition, 102(3), 361-395.
Στασινός, Δ. (2003) (Επιμ). Μαθησιακές δυσκολίες του παιδιού και του εφήβου. Η εμπειρία της σύγχρονης Ευρώπης. Αθήνα: Gutenberg.
Shams. L. & Seitz, A. R. (2008). Benefits of Multisensory Learning. Trends in Cognitive Sciences, 12(11), 411-417.
Wilson, A. J., & Dehaene, S. (2007). Number sense and developmental dyscalculia. Human behavior, learning and the developing brain: Atypical development, 2, 212-237.
Σημειώσεις από τα βιωματικά σεμινάρια του δρ. Καραγιαννάκη Ιωάννη: "Δυσαριθμησία: Στρατηγικές αντιμετώπισης των μαθησιακών δυσκολιών στα Μαθηματικά μαθητών πρωτοβάθμιας και δευτεροβάθμιας εκπαίδευσης" (17/10/2015) & "Αντιμετώπιση των δυσκολιών στα Μαθηματικά με έξυπνο τρόπο" (20/05/2017), Διεπιστημονικό Κέντρο Ηπείρου, Ιωάννινα.
Δευτέρα 9 Δεκεμβρίου 2019
Κυριακή 1 Δεκεμβρίου 2019
Δυσαριθμησία: Μέρος 2º - Προειδοποιητικά σημάδια και έγκαιρη διάγνωση
Για να διαβάσετε το πρώτο μέρος σχετικά με το τι είναι η δυσαριθμησία, πατήστε εδώ.
Τα "ύποπτα" σημάδια
Παλιότερα, εξαιτίας της άγνοιας γύρω από τη δυσαριθμησία, πολλά παιδιά αποτύγχαναν στα Μαθηματικά στο σχολείο και, σαν να μην έφτανε αυτό, συχνά νόμιζαν ότι έφταιγαν εκείνα για τις αποτυχίες τους. Στη σύγχρονη εποχή, γονείς και εκπαιδευτικοί έχουμε συνεχώς τα μάτια μας ανοιχτά για την πρώιμη ανίχνευση "ύποπτων" συμπτωμάτων, ώστε να απευθυνθούμε έγκαιρα στους ειδικούς. Κάποια από τα σημάδια που προειδοποιούν για την πιθανή ύπαρξη δυσαριθμησίας είναι τα εξής:
Για ένα παιδί ηλικίας έως 6 ετών:
- Δυσκολεύεται στο να μαθαίνει να μετρά.
- Δυσκολεύεται στο να αναγνωρίζει τα σύμβολα των αριθμών, π.χ. αδυνατεί να αντιστοιχίσει το σύμβολο "4" με τη λέξη "τέσσερα".
- Δυσκολεύεται να ακολουθήσει οδηγίες που περιλαμβάνουν αριθμούς, π.χ. "Δώσε μου δύο καραμέλες" ή "Φέρε τρεις μαρκαδόρους".
- Δυσκολεύεται να κατανοήσει την αξία των μονοψήφιων αριθμών, δηλαδή να αντιστοιχίζει το πλήθος κάποιων αντικειμένων με έναν αριθμό. Π.χ. δεν μπορεί με ευκολία να απαντήσει στην ερώτηση "Πόσα μπισκότα έμειναν;" ή απαντά συχνά λανθασμένα.
- Δυσκολεύεται στη χρήση χρονικών εννοιών, π.χ. σήμερα, αύριο, χθες.
- Δυσκολεύεται στη χρήση χωρικών εννοιών, π.χ. μπροστά, πίσω, πάνω, κάτω.
Για έναν μαθητή Δημοτικού:
- Συχνά λέει τους αριθμούς με λανθασμένη σειρά.
- Δυσκολεύεται στην εκτέλεση των τεσσάρων βασικών πράξεων (πρόσθεση, αφαίρεση, πολλαπλασιασμός, διαίρεση). Πιθανόν να μπερδεύει τα σύμβολα των πράξεων μεταξύ τους, όπως το + με το x, γεγονός που μπορεί να σχετίζεται με την ύπαρξη δυσλεξίας. Δυσκολεύεται να κατανοήσει τη διαφορά μεταξύ της πρόσθεσης και της αφαίρεσης.
- Δυσκολεύεται στην εκμάθηση της προπαίδειας με τον παραδοσιακό τρόπο. Αυτό επίσης σχετίζεται με τη δυσλεξία, γιατί το "ποίημα" της προπαίδειας είναι περισσότερο λεκτικό παρά αριθμητικό.
- Αποφεύγει τη χρήση των αριθμητικών συμβόλων, κάνοντας πρόσθεση ή αφαίρεση με τα δάχτυλα -ενώ οι συμμαθητές του έχουν σταματήσει να χρησιμοποιούν τη μέθοδο αυτή, χρησιμοποιώντας αντικείμενα ή ζωγραφίζοντας μικρές γραμμές στο χαρτί. Αυτές είναι στρατηγικές που πολλές φορές αναπτύσσουν μόνα τους τα παιδιά στην προσπάθειά τους να υπερβούν τις δυσκολίες τους και καλό είναι να μην αποθαρρύνονται από εμάς όταν τις εφαρμόζουν.
- Δυσκολεύεται στην κατανόηση μαθηματικών προβλημάτων και στη διαδικασία επίλυσής τους.
- Ακόμη κι αν γνωρίζει τη λύση σε ένα πρόβλημα, ίσως είναι αργό στην εκτέλεση των πράξεων με χαρτί και μολύβι. Αυτό πιθανόν να σχετίζεται με τη δυσλεξία και συμβαίνει διότι το παιδί δεν βασίζεται στον τυπικό χειρισμό των αριθμών, αλλά προτιμά έναν "δικό του" τρόπο συλλογισμού, όπου χρησιμοποιεί τις οπτικοχωρικές του δεξιότητες για να οπτικοποιήσει το πρόβλημα. Στην περίπτωση αυτή, το παιδί πρέπει να ενθαρρύνεται στη χρήση των οπτικοχωρικών του δεξιοτήτων. Οι δεξιότητες αυτές μπορούν αργότερα, κατά τη δευτεροβάθμια εκπαίδευση, να το βοηθήσουν να υπερέχει στα ανώτερα μαθηματικά όπως η τριγωνομετρία και η Ευκλείδεια Γεωμετρία.
- Δυσκολεύεται να μάθει τη μαθηματική ορολογία, π.χ. άθροισμα, γινόμενο, πηλίκο, εκατοστό.
- Παρουσιάζει ελλείμματα στη μνήμη εργασίας και στη βραχύχρονη μνήμη. Έχει, για παράδειγμα, τη δυσκολία να μην ενθυμείται το είδος της μαθηματικής πράξης που βρίσκεται σε εξέλιξη (π.χ. πρόσθεση), με αποτέλεσμα να τη μετατρέπει σε άλλη (π.χ. αφαίρεση).
- Δυσκολεύεται στη σειροθέτηση, π.χ. να λέει τις ημέρες της εβδομάδας ή τους μήνες με τη σειρά.
- Δυσκολεύεται να θυμάται γεγονότα με τη σειρά κατά την οποία συνέβησαν.
- Δυσκολεύεται να μάθει να λέει την ώρα κοιτώντας το αναλογικό ρολόι.
- Δυσκολεύεται στο να κρατάει το σκορ κατά τη διάρκεια ενός παιχνιδιού.
- Δυσκολεύεται στη χρήση χωρικών εννοιών, π.χ. δεξιά, αριστερά.
- Δυσκολεύεται να μάθει τα σημεία του ορίζοντα (Βορράς, Νότος, Δύση, Ανατολή) και γενικότερα να προσανατολίζεται.
- Δυσκολεύεται στο να ταξινομεί αντικείμενα ως προς το σχήμα ή το χρώμα ή το μέγεθός τους.
- Παρουσιάζει άγχος και μαθηματική φοβία εξαιτίας των δυσκολιών του με τους αριθμούς, παραπονιέται ότι δεν νιώθει καλά όταν έχει να λύσει ασκήσεις Μαθηματικών.
Για έναν έφηβο ή ενήλικα:
- Δυσκολεύεται στην εκτίμηση του κόστους ενός προϊόντος.
- Δυσκολεύεται στην κατανόηση και στη χρήση των ποσοστών.
- Δυσκολεύεται να εφαρμόσει τα κλάσματα στην καθημερινή ζωή, π.χ. τα 10 λεπτά του ευρώ είναι το ένα δέκατο του ευρώ ή 6 μήνες είναι μισό έτος.
- Δυσκολεύεται στη διαχείριση των χρημάτων, π.χ. να υπολογίσει σωστά τα ρέστα και στην κατανόηση της αξίας τους.
- Δυσκολεύεται στη διαχείριση και στην οργάνωση του χρόνου του.
- Αντιμετωπίζει πρόβλημα συνέπειας στην ώρα.
- Δυσκολεύεται στην οργάνωση του χώρου.
- Δυσκολεύεται στον προσανατολισμό και να ακολουθεί χάρτες. Ενδεχόμενες δυσκολίες στον προσανατολισμό και στη διαχείριση των χωρικών εννοιών μπορούν να επηρεάσουν αρνητικά την οδήγηση ενός οχήματος.
- Δυσκολεύεται να διαβάσει μια γραφική παράσταση ή ένα στατιστικό διάγραμμα, π.χ. ένα ραβδόγραμμα.
- Δυσκολεύεται στην επίλυση μαθηματικών προβλημάτων και γενικότερα προβλημάτων που περιλαμβάνουν αριθμούς.
Διάγνωση της δυσαριθμησίας
Πρέπει να τονιστεί ότι οι παραπάνω ενδείξεις είναι απλώς προειδοποιητικά σημάδια και σε καμία περίπτωση δεν αποτελούν διαγνωστικά κριτήρια για τη δυσαριθμησία, η διάγνωση/διαφοροδιάγνωση της οποίας γίνεται αποκλειστικά από τον αρμόδιο διαγνωστικό φορέα. Σήμερα στη χώρα μας, ο αρμόδιος κρατικός φορέας είναι τα Κέντρα Εκπαιδευτικής και Συμβουλευτικής Υποστήριξης (Κ.Ε.Σ.Υ.). Σε περίπτωση διάγνωσης δυσαριθμησίας ή άλλης ειδικής μαθησιακής δυσκολίας, οι γονείς καταθέτουν τη διάγνωση στο σχολείο όπου φοιτά το παιδί, ώστε να εξετάζεται με τον τρόπο που του ταιριάζει. Εκτός από τα Κ.Ε.Σ.Υ., υπάρχει και πληθώρα ιδιωτικών κέντρων για διάγνωση και παρέμβαση. Στα ιδιωτικά κέντρα, σε αντίθεση με τα Κ.Ε.Σ.Υ., οι γονείς έχουν άμεσα μια αξιολόγηση για το παιδί τους. Η ιδιωτική, όμως, διάγνωση δεν μπορεί να κατατεθεί στο σχολείο του παιδιού.
Μια ακριβής διάγνωση γίνεται μόνο μέσω μιας κλινικής αξιολόγησης από τη διεπιστημονική ομάδα, η οποία χορηγεί στο παιδί ειδικά τεστ (WISC, Αθηνά-Test κ.ά.), σταθμισμένα για την εκάστοτε ηλικία. Όσο πιο νωρίς γίνεται η διάγνωση, τόσο το καλύτερο, γιατί δεν περιμένουμε τη σχολική αποτυχία ώστε να κινητοποιηθούμε, αλλά δρούμε προληπτικά και παρεμβαίνουμε πρώιμα στις δυσκολίες του παιδιού.
Βιβλιογραφία
Αγαλιώτης, Ι. (2000). Μαθησιακές Δυσκολίες στα Μαθηματικά. Αιτιολογία, αξιολόγηση, αντιμετώπιση. Αθήνα: Ελληνικά Γράμματα.
Hannel, G. (2013) (2nd edition). Dyscalculia: Action plans for successful learning in Mathematics. New York: Routledge.
Karagiannakis, G., & Baccaglini-Frank, A. (2014). The De-Di-Ma battery: A tool for identifying students' mathematical learning profiles. Health Psychology Review, 2(4), 291-297.
Κουλάκογλου, Κ. (2017). Ψυχομετρία και Ψυχολογική Αξιολόγηση. Αθήνα: Πατάκη.
Rousselle, L., & Noel. M. P. (2007). Basic numerical skills in children with mathematics learning disabilities: A comparison of symbolic vs non-symbolic number magnitude processing. Cognition, 102(3), 361-395.
Στασινός, Δ. (2003) (Επιμ). Μαθησιακές δυσκολίες του παιδιού και του εφήβου. Η εμπειρία της σύγχρονης Ευρώπης. Αθήνα: Gutenberg.
Wilson, A. J., & Dehaene, S. (2007). Number sense and developmental dyscalculia. Human behavior, learning and the developing brain: Atypical development, 2, 212-237.
Σημειώσεις από τα βιωματικά σεμινάρια του δρ. Καραγιαννάκη Ιωάννη: "Δυσαριθμησία: Στρατηγικές αντιμετώπισης των μαθησιακών δυσκολιών στα Μαθηματικά μαθητών πρωτοβάθμιας και δευτεροβάθμιας εκπαίδευσης" (17/10/2015) & "Αντιμετώπιση των δυσκολιών στα Μαθηματικά με έξυπνο τρόπο" (20/05/2017), Διεπιστημονικό Κέντρο Ηπείρου, Ιωάννινα.
Hannel, G. (2013) (2nd edition). Dyscalculia: Action plans for successful learning in Mathematics. New York: Routledge.
Karagiannakis, G., & Baccaglini-Frank, A. (2014). The De-Di-Ma battery: A tool for identifying students' mathematical learning profiles. Health Psychology Review, 2(4), 291-297.
Κουλάκογλου, Κ. (2017). Ψυχομετρία και Ψυχολογική Αξιολόγηση. Αθήνα: Πατάκη.
Rousselle, L., & Noel. M. P. (2007). Basic numerical skills in children with mathematics learning disabilities: A comparison of symbolic vs non-symbolic number magnitude processing. Cognition, 102(3), 361-395.
Στασινός, Δ. (2003) (Επιμ). Μαθησιακές δυσκολίες του παιδιού και του εφήβου. Η εμπειρία της σύγχρονης Ευρώπης. Αθήνα: Gutenberg.
Wilson, A. J., & Dehaene, S. (2007). Number sense and developmental dyscalculia. Human behavior, learning and the developing brain: Atypical development, 2, 212-237.
Σημειώσεις από τα βιωματικά σεμινάρια του δρ. Καραγιαννάκη Ιωάννη: "Δυσαριθμησία: Στρατηγικές αντιμετώπισης των μαθησιακών δυσκολιών στα Μαθηματικά μαθητών πρωτοβάθμιας και δευτεροβάθμιας εκπαίδευσης" (17/10/2015) & "Αντιμετώπιση των δυσκολιών στα Μαθηματικά με έξυπνο τρόπο" (20/05/2017), Διεπιστημονικό Κέντρο Ηπείρου, Ιωάννινα.
Παρασκευή 22 Νοεμβρίου 2019
Δυσαριθμησία: Μέρος 1º - Τι είναι η δυσαριθμησία; Ο ρόλος της προληπτικής διδασκαλίας
Αποφάσισα να δημοσιεύσω στο ιστολόγιο μια σειρά άρθρων σχετικά με τη δυσαριθμησία, επειδή είναι ένα θέμα που απασχολεί πολλούς γονείς και εκπαιδευτικούς. Ελπίζω να φανούν χρήσιμα σε όσους ενδιαφέρονται.
Τι είναι η δυσαριθμησία;
Η δυσαριθμησία αποτελεί μια ειδική μαθησιακή δυσκολία που αναφέρεται στην εκμάθηση και την κατανόηση της αριθμητικής και της περαιτέρω ανάπτυξης των μαθηματικών δεξιοτήτων. Συμπεριλαμβάνεται στην "ομπρέλα" του γενικότερου όρου της δυσλεξίας. Συγκεκριμένα, ένας μαθητής με δυσαριθμησία δυσκολεύεται στην εκμάθηση της χρήσης των αριθμών και στην εκτέλεση μαθηματικών πράξεων. Επιπλέον, μπορεί να αντιμετωπίζει δυσκολίες όσον αφορά την έκφραση των σχέσεων μεταξύ ποσοτήτων, οι οποίες εκπροσωπούνται από αριθμούς, μεταβλητές ή άλλα σύμβολα.
Η ιδιαίτερη φύση της δυσαριθμησίας
Η δυσαριθμησία και γενικότερα οι ειδικές μαθησιακές δυσκολίες δεν πρέπει να συγχέονται με τις λεγόμενες δυσκολίες στη μάθηση που ενδέχεται να αντιμετωπίζει ένα παιδί που δεν έχει διδαχτεί κατάλληλα και επαρκώς κάποιες μαθηματικές έννοιες και που παρουσιάζει ορισμένα "κενά" στην ύλη που θα έπρεπε να γνωρίζει. Οι τελευταίες μπορούν να ξεπεραστούν πολύ εύκολα με λίγες επιπλέον ώρες διδασκαλίας και λίγη επιπλέον προσπάθεια από το παιδί, σε αντίθεση με τις ειδικές μαθησιακές δυσκολίες που απαιτούν το κατάλληλο πρόγραμμα παρέμβασης από ειδικό εκπαιδευτικό, έπειτα από τη σχετική διάγνωση/διαφοροδιάγνωση από τον αρμόδιο διαγνωστικό φορέα.
Όπως για όλες τις ειδικές μαθησιακές δυσκολίες, έτσι και για τη δυσαριθμησία, δεν υπάρχει κάποια "θεραπεία". Η δυσαριθμησία δεν είναι μια "φάση" την οποία το παιδί θα ξεπεράσει. Είναι ο τρόπος με τον οποίο ο εγκέφαλός του δημιουργεί συνδέσεις και επεξεργάζεται τα Μαθηματικά. Όπως και το χρώμα των ματιών του, αποτελεί ένα κομμάτι του εαυτού του και θα το συντροφεύει σε όλη του τη ζωή. Ο σκοπός της έγκαιρης διάγνωσης και παρέμβασης είναι να γεμίσουμε όσο το δυνατόν περισσότερα κενά και να το βοηθήσουμε να υπερβεί τις δυσκολίες του, αναπτύσσοντας τους δικούς του μηχανισμούς που θα χρησιμοποιεί, όχι μόνο στα σχολικά του χρόνια, αλλά και σε οποιαδήποτε κατάσταση χρειάζεται τα Μαθηματικά στη ζωή του.
Δυστυχώς, εξαιτίας της άγνοιας περί ειδικών μαθησιακών δυσκολιών που επικρατούσε παλιότερα, ούτε και οι εκπαιδευτικοί ήταν ενήμεροι για τη δυσαριθμησία. Απέδιδαν τις δυσκολίες του παιδιού και την αδυναμία του να διεκπεραιώσει μια άσκηση σε αδιαφορία, τεμπελιά ή απλώς σε μειωμένη μαθηματική ικανότητα! Παρόλα αυτά, σύμφωνα με σχετικές έρευνες, ο δείκτης νοημοσύνης ενός παιδιού με δυσαριθμησία είναι συνήθως κανονικός, ή ακόμη και σε ανώτερο επίπεδο, γεγονός που καταρρίπτει τους παλιότερους μύθους.
Ο ρόλος της προληπτικής διδασκαλίας
Προσωπικά, δεν είχα ακούσει ποτέ για τη δυσαριθμησία και για τους τρόπους παρέμβασης όσο το παιδί μου ήταν στην προσχολική ηλικία. Όμως, ως μια μαμά που λατρεύει τα Μαθηματικά, άρπαζα κάθε ευκαιρία να ενθέσω μια μικρή μαθηματική διδασκαλία κατά τη διάρκεια του παιχνιδιού, από το μέτρημα των μαρκαδόρων μας και την "ανακάλυψη" γεωμετρικών σχημάτων παντού, μέχρι τραγούδια με αριθμούς! Κατά τα σχολικά χρόνια, μαθαίναμε την πρόσθεση μέσα από χειροτεχνίες και παίζαμε με την προπαίδεια. Τελικά, ίσως αυτό είναι που χρειάζονται τα παιδιά, με ή χωρίς δυσαριθμησία -να διδάσκονται τα μαθηματικά με εναλλακτικούς, μη συμβατικούς τρόπους. Και, παρόλο που στη δική μας περίπτωση δεν εμφανίστηκαν ποτέ μαθησιακές δυσκολίες, εντούτοις όλες εκείνες οι δραστηριότητες θα μπορούσαν να φανούν ιδιαίτερα χρήσιμες στην περίπτωση δυσαριθμησίας ή άλλων ειδικών μαθησιακών δυσκολιών. Μέσα από εκπαιδευτικά παιχνίδια, από την προσχολική ηλικία, μπορούμε να δρούμε προληπτικά απέναντι σε όποια ειδική μαθησιακή δυσκολία μπορεί να υπάρχει, χωρίς να περιμένουμε να δούμε το παιδί να αποτυγχάνει στο σχολείο για να αποφασίσουμε να απευθυνθούμε στους ειδικούς. Αντιμετωπίζουμε, έτσι, τυχόντα προβλήματα προτού αυτά επιδεινωθούν. Χάρη στην προληπτική διδασκαλία, επωφελούνται τελικά όλα τα παιδιά, όχι μόνο εκείνα με δυσαριθμησία, αφού κάθε παιδί έχει τις προσωπικές του προτιμήσεις, ανάγκες και επιθυμίες, ικανότητες και αδυναμίες. Έχει τον δικό του, εξατομικευμένο τρόπο μάθησης.
Βιβλιογραφία
Αγαλιώτης, Ι. (2000). Μαθησιακές Δυσκολίες στα Μαθηματικά. Αιτιολογία, αξιολόγηση, αντιμετώπιση. Αθήνα: Ελληνικά Γράμματα.
Hannel, G. (2013) (2nd edition). Dyscalculia: Action plans for successful learning in Mathematics. New York: Routledge.
Karagiannakis, G., & Baccaglini-Frank, A. (2014). The De-Di-Ma battery: A tool for identifying students' mathematical learning profiles. Health Psychology Review, 2(4), 291-297.
Rousselle, L., & Noel. M. P. (2007). Basic numerical skills in children with mathematics learning disabilities: A comparison of symbolic vs non-symbolic number magnitude processing. Cognition, 102(3), 361-395.
Στασινός, Δ. (2003) (Επιμ). Μαθησιακές δυσκολίες του παιδιού και του εφήβου. Η εμπειρία της σύγχρονης Ευρώπης. Αθήνα: Gutenberg.
Wilson, A. J., & Dehaene, S. (2007). Number sense and developmental dyscalculia. Human behavior, learning and the developing brain: Atypical development, 2, 212-237.
Σημειώσεις από τα βιωματικά σεμινάρια του δρ. Καραγιαννάκη Ιωάννη: "Δυσαριθμησία: Στρατηγικές αντιμετώπισης των μαθησιακών δυσκολιών στα Μαθηματικά μαθητών πρωτοβάθμιας και δευτεροβάθμιας εκπαίδευσης" (17/10/2015) & "Αντιμετώπιση των δυσκολιών στα Μαθηματικά με έξυπνο τρόπο" (20/05/2017), Διεπιστημονικό Κέντρο Ηπείρου, Ιωάννινα.
Hannel, G. (2013) (2nd edition). Dyscalculia: Action plans for successful learning in Mathematics. New York: Routledge.
Karagiannakis, G., & Baccaglini-Frank, A. (2014). The De-Di-Ma battery: A tool for identifying students' mathematical learning profiles. Health Psychology Review, 2(4), 291-297.
Rousselle, L., & Noel. M. P. (2007). Basic numerical skills in children with mathematics learning disabilities: A comparison of symbolic vs non-symbolic number magnitude processing. Cognition, 102(3), 361-395.
Στασινός, Δ. (2003) (Επιμ). Μαθησιακές δυσκολίες του παιδιού και του εφήβου. Η εμπειρία της σύγχρονης Ευρώπης. Αθήνα: Gutenberg.
Wilson, A. J., & Dehaene, S. (2007). Number sense and developmental dyscalculia. Human behavior, learning and the developing brain: Atypical development, 2, 212-237.
Σημειώσεις από τα βιωματικά σεμινάρια του δρ. Καραγιαννάκη Ιωάννη: "Δυσαριθμησία: Στρατηγικές αντιμετώπισης των μαθησιακών δυσκολιών στα Μαθηματικά μαθητών πρωτοβάθμιας και δευτεροβάθμιας εκπαίδευσης" (17/10/2015) & "Αντιμετώπιση των δυσκολιών στα Μαθηματικά με έξυπνο τρόπο" (20/05/2017), Διεπιστημονικό Κέντρο Ηπείρου, Ιωάννινα.
Παρασκευή 1 Νοεμβρίου 2019
Γρίφος: Η κάτοψη της πυραμίδας
Παρατηρήστε την πυραμίδα της εικόνας και προσπαθήστε να φανταστείτε πώς θα φαίνεται κοιτώντας την ακριβώς από πάνω...
Για να μάθετε περισσότερα για την πυραμίδα, πατήστε εδώ...
Σάββατο 26 Οκτωβρίου 2019
Τετάρτη 9 Οκτωβρίου 2019
Τουλάχιστον μία λύση...
Το Θεώρημα του Bolzano
Έστω μια συνάρτηση f, ορισμένη σ' ένα κλειστό διάστημα [α, β]. Αν ισχύουν τα εξής:
- η f είναι συνεχής στο [α, β] και
- f(α)⋅f(β) < 0,
τότε υπάρχει ένα τουλάχιστον x0 στο ανοιχτό διάστημα (α, β) τέτοιο, ώστε
f(x0) = 0
Δηλαδή το Θεώρημα Bolzano μας εξασφαλίζει ότι υπάρχει μία τουλάχιστον λύση της εξίσωσης f(x) = 0 στο ανοιχτό διάστημα (α, β).
Τρίτη 1 Οκτωβρίου 2019
Γρίφος: Συσκευάζοντας μαρμελάδες
Στη βιοτεχνία όπου εργάζεσαι, σου ζήτησαν να στείλεις κυλινδρικά βάζα μαρμελάδας, διαμέτρου 10 εκ. Θέλεις να σχεδιάσεις ένα κυλινδρικό κουτί για να συσκευάζεις τα βάζα μαρμελάδας, ίδιου ύψους με τα βάζα, ώστε κάθε κουτί να χωράει 7 βάζα. Καλείσαι, λοιπόν, να λύσεις το εξής γεωμετρικό πρόβλημα:
Ποια είναι η ελάχιστη εσωτερική διάμετρος που πρέπει να έχει το κουτί;
 |
| (Πηγή) |
Τετάρτη 11 Σεπτεμβρίου 2019
Δευτέρα 2 Σεπτεμβρίου 2019
Ποιοι είναι οι μαθητές μου;
Μαθησιακά προφίλ και προσαρμογή της διδασκαλίας
Ο Άλμπερτ Αινστάιν συχνά ονειροπολούσε μέσα
στο μάθημα, ενώ πιστεύεται από πολλούς ότι αντιμετώπιζε ειδικές μαθησιακές
δυσκολίες. Ο Τόμας Έντισον, όντας ανήσυχο πνεύμα, είχε τιμωρηθεί τόσες πολλές
φορές από τους δασκάλους του, που η μητέρα του αναγκάστηκε να τον κρατήσει
μακριά από το σχολείο. Ο Δαρβίνος, ο Λεονάρντο vτα Βίντσι και η Αγκάθα Κρίστι
είναι ακόμη μερικά παραδείγματα ανθρώπων που οι μαθησιακές δυσκολίες τους
συντρόφευαν σε ολόκληρη τη ζωή τους. Παρόλα αυτά, όλοι τους έχουν αφήσει
παντοτινά το στίγμα τους στην παγκόσμια ιστορία της επιστήμης και της τέχνης.
Κάθε παιδί, είτε αντιμετωπίζει μαθησιακές
δυσκολίες είτε όχι, έχει διαφορετικά ταλέντα, διαφορετικές ανάγκες, διαφορετικό
τρόπο έκφρασης και διαφορετικό μαθησιακό στυλ. Με τον όρο «μαθησιακό στυλ»
εννοούμε τον τρόπο με τον οποίο οι άνθρωποι συγκεντρώνουν, κατανοούν και
συγκρατούν καινούριες πληροφορίες. Έτσι, κάθε παιδί είναι μοναδικό, όπως
μοναδικός είναι και ο τρόπος με τον οποίο κατακτά τη γνώση. Κάποιοι μαθητές
νιώθουν εξοικειωμένοι με τη χρήση εικόνων και γραφικών παραστάσεων, άλλοι είναι
άνετοι κατά την ακρόαση διαλέξεων ή στις ομαδικές συζητήσεις, άλλοι προτιμούν
τη μάθηση μέσα από την ανάγνωση ή την αντιγραφή κειμένων, ενώ άλλοι αποδίδουν
καλύτερα κατά την ενεργητική μάθηση και κατανοούν τις πληροφορίες που
προσλαμβάνουν μέσα από πρακτικές δραστηριότητες. Υπάρχουν τέσσερις βασικοί
τύποι μάθησης όσον αφορά τον αισθητηριακό τομέα: ο οπτικός, ο ακουστικός, ο
αναγνωστικός/λεκτικός, και ο κιναισθητικός. Ο προσωπικός τρόπος μάθησης του
κάθε παιδιού αποτελεί συνδυασμό των παραπάνω τύπων.
Κατά την εκπαίδευση των μαθητών μας, λοιπόν,
οι ειδικοί επιστήμονες συστήνουν δοκιμασμένους τρόπους για το πώς μπορούμε να
προσαρμόσουμε τη διδασκαλία του μαθήματος, σύμφωνα με τις ατομικές ικανότητες των παιδιών και να
επιστρατεύσουμε εναλλακτικές μεθόδους διδασκαλίας. Απαιτείται να λαμβάνουμε
υπόψη μας το βαθμό ετοιμότητας των μαθητών, τα ενδιαφέροντά τους και το
μαθησιακό τους στυλ καθώς διαφοροποιούμε τη διδασκαλία. Έχει αποδειχθεί,
επίσης, ότι οι μαθητές έχουν καλύτερη επίδοση και πιο θετική στάση αν
διδάσκονται με τρόπους που μπορούν να κατανοήσουν πιο εύκολα.
Κλείνοντας, δεν υπάρχει ένας συγκεκριμένος
τρόπος διδασκαλίας, ούτε ένας συγκεκριμένος τρόπος μάθησης. Γι’ αυτό οφείλουμε
να ενθαρρύνουμε τα παιδιά να δοκιμάζουν διάφορες τεχνικές, μέχρι να βρουν την
πιο κατάλληλη για αυτά και σε καμία περίπτωση να μην τα αναγκάζουμε να
εφαρμόζουν αποκλειστικά τις μεθόδους με τις οποίες είμαστε οι ίδιοι
εξοικειωμένοι. Στην τελική, όλοι βγαίνουν κερδισμένοι, αφού θα διαπιστώσουμε
πόσα πράγματα μπορούμε να μάθουμε διδάσκοντας τα παιδιά.
«Αν το παιδί δεν μπορεί να μάθει με τον τρόπο που το
διδάσκουμε,
τότε πρέπει να το διδάξουμε με τον τρόπο που μπορεί να μάθει».
τότε πρέπει να το διδάξουμε με τον τρόπο που μπορεί να μάθει».
(Μαρία Μοντεσσόρι)
*~.~*~.~*~.~*
*~.~*~.~*~.~*
Βιβλιογραφία
Reid, M. J. (1995). Learning styles
in the ESL/ EFL classroom. Boston: Heinle & Heinle.
Στασινός, Δ. (2003) (Επιμ). Μαθησιακές δυσκολίες του παιδιού και του εφήβου. Η εμπειρία
της σύγχρονης Ευρώπης. Αθήνα: Gutenberg.
Tomlinson, C.A. (2010). Διαφοροποίηση της
Εργασίας στην Αίθουσα Διδασκαλίας: Ανταπόκριση στις Ανάγκες Όλων των Μαθητών
(Μτφρ. X.
Θεοφιλίδης). Αθήνα:
Γρηγόρη.
Τετάρτη 21 Αυγούστου 2019
Ο Πόε για τη μαθηματική ανάλυση
Ο Έντγκαρ Άλλαν Πόε (1809 - 1849) ήταν Αμερικανός ποιητής και πεζογράφος και, προσωπικά, ένας από τους αγαπημένους μου. Το έργο του είχε σημαντική επιρροή στην παγκόσμια λογοτεχνία, αποτελώντας θεμέλιο λίθο για την εξέλιξη της αστυνομικής λογοτεχνίας, αλλά και τη λογοτεχνία τρόμου και φαντασίας.
Στο διήγημα μυστηρίου "Οι φόνοι στην οδό Νεκροτομείου" (Murders in the Rue Morgue, 1841) διαβάζει κανείς:
"Η αναλυτική ικανότητα ενισχύεται σημαντικά με τη μελέτη των μαθηματικών και ειδικά του υψηλότερου κλάδου τους που, αδίκως πάντως, μόνο και μόνο λόγω της παλινδρομικής του λειτουργίας ονομάζεται ανάλυση. Μια πράξη υπολογισμού δεν συνιστά ανάλυση..."
Σάββατο 3 Αυγούστου 2019
Κουίζ σε πίνακα
Σ' αυτόν τον πίνακα, κάθε σχήμα έχει μία συγκεκριμένη τιμή. Οι αριθμοί δίπλα σε κάθε γραμμή και κάτω από κάθε στήλη είναι το άθροισμα των τιμών στη γραμμή ή τη στήλη αντίστοιχα.
Τρίτη 30 Ιουλίου 2019
Τα Μαθηματικά στην Τέχνη: Αρχιμήδεια στερεά και διάφορα κυρτά πολύεδρα
Στην προηγούμενη ανάρτηση του πρότζεκτ "Τα Μαθηματικά στην Τέχνη" είδαμε τα πέντε κανονικά πολύεδρα, που ονομάστηκαν και πλατωνικά στερεά. Αυτό που τα καθιστά ξεχωριστά είναι το γεγονός ότι οι έδρες τους είναι όλες κανονικά πολύγωνα του ίδιου τύπου. Η επόμενη κατηγορία πολυέδρων είναι τα ημικανονικά πολύεδρα ή αλλιώς αρχιμήδεια στερεά...
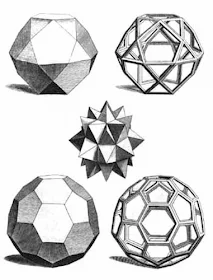
 |
| Σχέδια διαφόρων πολυέδρων. Από το βιβλίο του Max Brückner "Πολύγωνα και Πολύεδρα: Θεωρία και Ιστορία", 1900. |
Σύμφωνα με μαρτυρία του Πάππου, ο Αρχιμήδης στη χαμένη πραγματεία του για τα λεγόμενα ημικανονικά πολύεδρα, διακρίνει μια νέα κατηγορία πολυέδρων.
Τα βιβλία γράφουν...
Τα αρχιμήδεια στερεά (ή στερεά του Αρχιμήδη) είναι ημικανονικά κυρτά πολύεδρα, οι έδρες των οποίων είναι κανονικά πολύγωνα, αλλά όχι όλες του ίδιου τύπου. Τα κανονικά πολύγωνα που αποτελούν τις έδρες έχουν όλα ίσες τις πλευρές τους, δηλαδή οι ακμές κάθε αρχιμήδειου πολυέδρου είναι όλες ίσες. Οι έδρες ενώνονται με τον ίδιο ακριβώς τρόπο σε όλες τις κορυφές του πολυέδρου, διαμορφώνοντας ίσες πολυεδρικές γωνίες. Υπάρχουν 13 αρχιμήδεια στερεά:
Κόλουρο Τετράεδρο
Έχει 8 έδρες: 4 τρίγωνα και 4 εξάγωνα.
Ο όρος "κόλουρο" αναφέρεται στη διαδικασία της αποκοπής των κορυφών από ένα αρχικό πολύεδρο. Έτσι, κατασκευαστικά, το κόλουρο τετράεδρο προέρχεται από ένα τετράεδρο, από το οποίο έχουμε αποκόψει τις 4 κορυφές.
 |
| Σχέδιο του Leonardo da Vinci για το βιβλίο του Luca Paccioli "De Divina Proportione" (1509) |
Kυβοκτάεδρο
Έχει 14 έδρες: 8 τρίγωνα και 6 τετράγωνα.
 |
| Σχέδιο του Leonardo da Vinci για το βιβλίο του Luca Paccioli "De Divina Proportione" (1509) |
 |
| Ana Conde (Σύγχρονη ζωγράφος και tattoo artist) - "Cuboctahedron Full of Dust Bunnies" (2018) |
 |
| James Sawyer (Σύγχρονος καλλιτέχνης) - "Octahedron Inside a Cuboctahedron" (2010) |
Κόλουρος Κύβος ή Κόλουρο Εξάεδρο
Έχει 14 έδρες: 8 τρίγωνα και 6 οκτάγωνα.
 |
| Άγνωστος καλλιτέχνης από τις Η.Π.Α. - "Truncated Cube, Possibly a Zodiac Instrument" |
Κόλουρο Οκτάεδρο
Έχει 14 έδρες: 6 τετράγωνα και 8 κανονικά εξάγωνα.
Κατασκευαστικά, προέρχεται από το οκτάεδρο, αν αποκοπούν όλες οι κορυφές του στο 1/3 της ακμής, έτσι ώστε από τις έδρες του αρχικού οκτάεδρου να προκύψουν εξάγωνα και στη θέση των αποκομμένων κορυφών του να σχηματιστούν τετράγωνα.
"Octocedron Abscisus Vacuus"
Σχέδιο του Leonardo da Vinci για το βιβλίο του Luca Paccioli "De Divina Proportione" (1509) |
Ρομβοκυβοκτάεδρο (ή μικρό ρομβοκυβοκτάεδρο)
Έχει 26 έδρες: 8 τρίγωνα και 18 τετράγωνα.
 |
| "Vigintisex Basilum Planus Vacuus" Σχέδιο του Leonardo da Vinci για το βιβλίο του Luca Paccioli "De Divina Proportione" (1509) |
 |
| Η πρώτη τυπωμένη απεικόνιση ενός ρομβοκυβοκτάεδρου. Έργο του Leonardo da Vinci, στο βιβλίο του Luca Paccioli, "De Divina Proportione" (1509) |
Κόλουρο Κυβοκτάεδρο (ή μέγα ρομβοκυβοκτάεδρο)
Έχει 26 έδρες: 12 τετράγωνα, 8 εξάγωνα και 6 οκτάγωνα.
 |
| Jim Wrenholt (Σύγχρονος graphic designer) - "Truncated Cuboctahedron" (2014) |
Πεπλατυσμένος κύβος (ή πεπλατυσμένο εξάεδρο)
Ο όρος "πεπλατυσμένος" αναφέρεται στη διαδικασία της "επέκτασης" του αρχικού σχήματος. Κατασκευαστικά, ο πεπλατυσμένος κύβος μπορεί να προέλθει από τον κύβο, αν απομακρύνουμε όλες τις έδρες του προς τα έξω, κατά ορισμένη απόσταση και τις περιστρέψουμε ως προς το κέντρο τους έτσι, ώστε τα κενά που δημιουργούνται να μπορούν να καλυφθούν από ισόπλευρα τρίγωνα.
 |
| Γλυπτό-συντριβάνι σε σχήμα πεπλατυσμένου κύβου. Διακοσμεί τον εξωτερικό χώρο του Caltech στην Καλιφόρνια. |
Εικοσιδωδεκάεδρο
Έχει 32 έδρες: 20 τρίγωνα και 12 πεντάγωνα.
 |
| Η πρώτη τυπωμένη απεικόνιση ενός εικοσιδωδεκάεδρου. Έργο του Leonardo da Vinci, στο βιβλίο του Luca Paccioli, "De Divina Proportione" (1509) |
 |
| P.S. (Σύγχρονος graphic designer) - "Icosidodecahedron 2" |
Κόλουρο δωδεκάεδρο
Έχει 32 έδρες: 20 τρίγωνα και 12 δεκάγωνα.
 |
| Jim Wrenholt (Σύγχρονος graphic designer) - "Truncated Dodecahedron" (2014) |
Κόλουρο εικοσάεδρο
Έχει 32 έδρες: 12 πεντάγωνα και 20 εξάγωνα. Το μοτίβο του κόλουρου εικοσάεδρου χρησιμοποιείται στην κατασκευή της συνηθισμένης μπάλας ποδοσφαίρου.
 |
| "Ycocedron Abscisus Vacuus" Σχέδιο του Leonardo da Vinci για το βιβλίο του Luca Paccioli "De Divina Proportione" (1509) |
 |
| Απόκρυφη Γεωμετρία της Αναγέννησης: Ένα ζευγάρι χέρια στηρίζει ένα κόλουρο εικοσάεδρο. Γλυπτό που διακοσμεί το ταφικό μνημείο του Sir Anthony Ashley, σε έναν ενοριακό ναό κοντά στο Salisbury, Αγγλία. |
Ρομβοεικοσιδωδεκάεδρο (ή μικρό ρομβοεικοσιδωδεκάεδρο)
Έχει 62 έδρες: 20 τρίγωνα, 30 τετράγωνα και 12 πεντάγωνα.
 |
| Jim Wrenholt (Σύγχρονος graphic designer) - "Rhombicosidodecahedron" (2014) |
Κόλουρο εικοσιδωδεκάεδρο (ή μέγα ρομβοεικοσιδωδεκάεδρο )
Έχει 62 έδρες: 30 τετράγωνα, 20 εξάγωνα και 12 δεκάγωνα.
 |
| Lindsey Carr (Σύγχρονη ζωγράφος) - "Jacques Great Rhombicosidodecahedron" |
Πεπλατυσμένο δωδεκάεδρο (ή πεπλατυσμένο εικοσιδωδεκάεδρο)
Έχει 92 έδρες: 80 τρίγωνα και 12 πεντάγωνα.
Κατασκευαστικά, το πεπλατυσμένο δωδεκάεδρο μπορεί να προέλθει με διαδικασία παρόμοια με εκείνη του πεπλατυσμένου κύβου, μόνο που τώρα το αρχικό στερεό είναι ένα δωδεκάεδρο.
 |
| Jim Wrenholt (Σύγχρονος graphic designer) - "Snub Dodecahedron" (2014) |
Τα βιβλία γράφουν...
Ο πρώτος που ασχολήθηκε με την κατασκευή αρχιμήδειων στερεών φαίνεται να ήταν ο Αρχιμήδης, ο οποίος τα διαπραγματευόταν στο (μη σωζόμενο) έργο του "Περί 13 ημικανονικών πολυέδρων" και γι' αυτό φέρουν το όνομά του. Ωστόσο, το όνομα κάθε αρχιμήδειου στερεού οφείλεται στον Kepler, που τα μελέτησε εκτενώς στο βιβλίο του "Αρμονικός Κόσμος" (Harmonices Mundi, 1619) και σήμερα έχουμε τη μεταφρασμένη, από τα λατινικά, ορολογία.
Διάφορα άλλα κυρτά πολύεδρα
Εννεάεδρο - Επιμήκης τετραγωνική πυραμίδα
Οι μικροί μαθητές πολύ ορθά το παρομοιάζουν με σπίτι!
 |
| Sabrina Barrios (Σύγχρονη καλλιτέχνιδα) - "Enneahedron" (2019) |
72εδρη σφαίρα (ή σφαίρα του Κάμπανου)
Το πολύεδρο αυτό προσεγγίζει τη σφαίρα και αποτελεί τη βάση για την κατασκευή αρχιτεκτονικών θόλων.
 |
| "Septuaginta Duarum Basilum Solidum" Σχέδιο του Leonardo da Vinci για το βιβλίο του Luca Paccioli "De Divina Proportione" (1509) |
 |
| "Septuaginta Duarum Basilum Vacuum" Σχέδιο του Leonardo da Vinci για το βιβλίο του Luca Paccioli "De Divina Proportione" (1509) |
Το στερεό του Dürer
Πρόκειται για το στερεό που διακρίνεται στο αριστερό κομμάτι της γκραβούρας του Albrecht Dürer, "Melencolia I":
Τα βιβλία γράφουν...
Για κάθε κυρτό πολύεδρο ισχύει ο τύπος του Euler:
K + E = A + 2,
όπου Κ το πλήθος των κορυφών του, Ε το πλήθος των εδρών του και Α το πλήθος των ακμών του.
Με άλλα λόγια, τα κυρτά πολύεδρα έχουν χαρακτηριστική Euler χ = Κ - Α + Ε = 2.
Με άλλα λόγια, τα κυρτά πολύεδρα έχουν χαρακτηριστική Euler χ = Κ - Α + Ε = 2.
Τα αρχιμήδεια στερεά, αλλά και πολλά άλλα πολύεδρα, παρουσιάζουν ποικίλες συμμετρίες και ομάδες συμμετρίας, οι οποίες μελετώνται από τη σύγχρονη Θεωρία Ομάδων. Εικάζεται ότι οι συμμετρίες αυτές είναι ο κύριος λόγος που ενέπνευσαν τόσο έντονα τους καλλιτέχνες, ειδικά κατά την Αναγέννηση. Ο καλλιτέχνης της Αναγέννησης που ασχολήθηκε διεξοδικότερα με τα πολύεδρα ήταν ο Leonardo da Vinci. Ειδικότερα, η τεχνοτροπία αναπαράστασης πολυέδρων που πρώτος χρησιμοποίησε, απεικονίζοντάς τα στέρεα και κοίλα, σαν ξύλινα μοντέλα (που πιθανότατα είχε κατασκευάσει για το σκοπό αυτό ο Luca Paccioli), ώστε να φαίνονται και οι "πίσω" ακμές, επηρέασε καθοριστικά όσους μεταγενέστερους ασχολήθηκαν με τα πολύεδρα στη ζωγραφική και γενικότερα στις εικαστικές τέχνες.
.*.〰.*.〰.*.〰.*.〰.*.〰.*.〰.*.
"Τα βασικά στοιχεία των μαθηματικών, οι αριθμοί και η μέτρηση, που ονομάστηκαν αριθμητική και γεωμετρία, χρησιμοποιούνται με υπέρτατη αλήθεια σε διακριτές αλλά και συνεχείς ποσότητες. Εδώ δε συναντάμε διαφωνίες, λόγου χάρη ότι 2 φορές το 3 μας κάνει περισσότερο ή λιγότερο από 6, ή ότι ένα τρίγωνο έχει άθροισμα γωνιών μικρότερο ή μεγαλύτερο από 2 ορθές, αλλά με αιώνια σιωπή, κάθε διαφωνία παύει να υφίσταται και, με ηρεμία, αυτές οι επιστήμες όπως τα μαθηματικά απολαμβάνονται από τους αφοσιωμένους τους ακολούθους".
Leonardo da Vinci
.*.〰.*.〰.*.〰.*.〰.*.〰.*.〰.*.
Πηγές:
- Ευκλείδεια Γεωμετρία Α' και Β' Γενικού Λυκείου, Ινστιτούτο Τεχνολογίας Υπολογιστών και Εκδόσεων "Διόφαντος", 2015
- E.H. Gombrich, Το Χρονικό της Τέχνης, Μορφωτικό Ίδρυμα Εθνικής Τραπέζης, 1995
- Πανεπιστημιακές σημειώσεις "Ιστορίας των Μαθηματικών" καθηγητή Α.Θωμά, 2010
- Flickr: Jim Wrenholt
- David Wade: Geometricism
- Leonardo da Vinci's Polyhedra
- http://www.matematicasvisuales.com/english/html/geometry/space/volcuboctahedron.html
- Wolfram Math World: Truncated Octahedron
- Universal Leonardo: Rule of Mathematics
- wikipedia.org