Κυριακή 22 Μαΐου 2022
Καλή επιτυχία στους μαθητές μας!
Τετάρτη 18 Μαΐου 2022
"Ο διαβήτης του Πλάτωνα"
Κατά τη διάρκεια του Πελοποννησιακού Πολέμου, η Δήλος προσβλήθηκε από λοιμό. Αντιπροσωπία πολιτών της ζήτησε χρησμό από το μαντείο των Δελφών. "Οι Δήλιοι και οι άλλοι Έλληνες θα ελευθερωθούν από τα παρόντα δεινά αν διπλασιάσουν τον κυβικό βωμό του θεού", προφήτεψε η Πυθία...
Βερολίνο 1929-1931. Ο νεαρός μαθηματικός Μπάρτελ βαν ντερ Βέρντεν εντοπίζει μια αντινομία στην "Πολιτεία" του Πλάτωνα, που τον φέρνει μέχρι την πόρτα του μεγάλου ελληνιστή φον Βιλαμόβιτς. Οι δύο άντρες θα ξεκινήσουν μαζί ένα ταξίδι στην ιστορία, σε αναζήτηση του νήματος ενός περίφημου μαθηματικού γρίφου, που παρέμενε άλυτος στην πορεία του χρόνου και της επιστήμης: του δηλίου προβλήματος, το οποίο σχετίζεται με τον διπλασιασμό του κύβου.
Με αγωνιώδη πλοκή και με αφήγηση που εναλλάσσεται από την κλασική Αθήνα στο Βερολίνο και το Γκέτινγκεν του Μεσοπολέμου, παραμονές ανόδου του Χίτλερ στην εξουσία, το μυθιστόρημα "Ο διαβήτης του Πλάτωνα" του Γιάννη Γρηγοράκη συνδυάζει με δεξιοτεχνία την πολιτική με τα μαθηματικά και ζωντανεύει δύο εποχές που σφράγισαν την παγκόσμια ιστορία.
Μεγάλες προσωπικότητες της επιστήμης και των γραμμάτων, από τον Πλάτωνα, τον Θεαίτητο, τον Εύδοξο και τον Αρχύτα τον Ταραντίνο, μέχρι τον Βιλαμόβιτς, τον βαν ντερ Βέρντεν, την Έμι Νέτερ και τον Γκάνταμερ, σκιαγραφούνται, παίρνουν μορφή και κινούνται αναζητώντας το νήμα του γρίφου.
Παρασκευή 13 Μαΐου 2022
Σε τι μας χρησιμεύουν τα μαθηματικά?
Για τους μαθητές που αναρωτιούνται πού θα χρειαστούν τα μαθηματικά στη ζωή τους, ο συνάδελφος Φώτης Καραμπουτάκης από το κανάλι Math Me Up εξηγεί με τη βοήθεια κινουμένων σχεδίων σε τι ακριβώς μας χρησιμεύουν τα μαθηματικά στην καθημερινή μας ζωή, αλλά και στον τρόπο που επηρεάζουν τον πολιτισμό μας και τον κόσμο γύρω μας.
Σάββατο 7 Μαΐου 2022
Γρίφος: Παράξενη αριθμομηχανή!
Ας υποθέσουμε ότι έχετε μια παράξενη αριθμομηχανή, η οποία μπορεί να εκτελέσει μόνο δύο πράξεις: Για κάθε δεδομένο ακέραιο αριθμό α, μπορεί να υπολογίσει το 2α + 1 ή το (α - 1)/3.
(Η δεύτερη πράξη είναι δυνατή μόνο όταν το α - 1 διαιρείται με το 3).
Μπορείτε, ξεκινώντας από το 1, να καταλήξετε με αυτή την αριθμομηχανή στο 8;
Πέμπτη 28 Απριλίου 2022
"Πυθαγόρεια εγκλήματα"
Αθήνα, 1929. Ο μαθηματικός Στέφανος Κανταρτζής βρίσκεται νεκρός στο δωμάτιό του. Ο επιστήθιος φίλος του, επίσης μαθηματικός, Μιχαήλ Ιγερινός, καλείται για να αναγνωρίσει το πτώμα. Όρθιος μπροστά στο νεκρό φίλο του, ο Ιγερινός αναπολεί τα κάπου τριάντα χρόνια της γνωριμίας τους: την πρώτη τους συνάντηση σ' ένα μαθηματικό συνέδριο το 1900, τις παρέες τους με τις αβάν γκαρντ της παρισινής διανόησης, τις περιπλανήσεις τους στο Παρίσι της Μπελ Επόκ, τους Βαλκανικούς Πολέμους, το Διχασμό, τη Μικρασιατική Καταστροφή. Θυμάται τις θυελλώδεις μαθηματικές τους διαφωνίες, τους έρωτές τους, τις πολεμικές τους περιπέτειες. Ο ήχος μιας ρομβίας τον επαναφέρει στο παρόν. Το ερώτημα είναι επιτακτικό: Ποιος σκότωσε τον Στεφανο Κανταρτζή, και κυρίως γιατί τον σκότωσε;
Μια αστυνομική περιπέτεια με έντονο μαθηματικό άρωμα, τα "Πυθαγόρεια εγκλήματα" του Τεύκρου Μιχαηλίδη αφηγούνται ένα φανταστικό έγκλημα με φόντο ένα αληθινό, σημαντικό φιλοσοφικό και μαθηματικό πρόβλημα.
Σάββατο 23 Απριλίου 2022
Δευτέρα 11 Απριλίου 2022
Ο αλγόριθμος υπολογισμού της ημερομηνίας του ορθόδοξου Πάσχα από τον Gauss
Πότε πέφτει φέτος το Πάσχα; Του χρόνου;
Στο βίντεο του μαθηματικού Θανάση Δρούγα (Μαθημαγικά) παρουσιάζεται ο αλγόριθμος του Gauss, με τον οποίο μπορούμε να βρούμε πότε πέφτει το Πάσχα των ορθοδόξων οποιαδήποτε χρονιά μέχρι το 2099.
Ο τύπος υπολογισμού της ημερομηνίας του Πάσχα είναι:
όπου \(x\) το έτος, \(H(x)\) η ημερομηνία που πέφτει το Πάσχα το έτος \(x\) και \(AmodB\) το υπόλοιπο της Ευκλείδειας Διαίρεσης του \(A\) με το \(B\).
Πατώντας εδώ: ("GeeksforGeeks"), μπορείτε να δείτε τον αλγόριθμο σε C++, Java, Python3, C#, Javascript.
Επαληθεύστε το για \(x=2022\) !
Τετάρτη 6 Απριλίου 2022
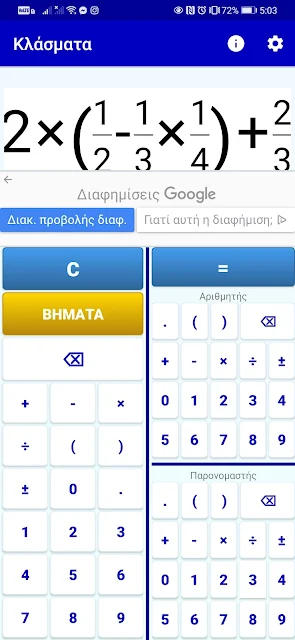
Fraction Calculator: Μια αριθμομηχανή Κλασμάτων για Android!
Οι Νέες Τεχνολογίες είναι πλέον αναπόσπαστο κομμάτι της σύγχρονης σχολικής πραγματικότητας και, εφόσον τα κινητά τηλέφωνα δεν λείπουν από κανέναν μαθητή, εμείς αποφασίσαμε να τα εκμεταλλευτούμε προς όφελος της μάθησης! Αυτός είναι και ο στόχος του m-Learning (ή mobile learning, κινητή μάθηση).
Αυτή τη φορά έχω να προτείνω την εφαρμογή για κινητά android, Fraction Calculator, που ανέπτυξε ο μαθηματικός Παντελής Μπουμπούλης. Πρόκειται για μια απλή και εύχρηστη αριθμομηχανή για πράξεις μεταξύ κλασμάτων. Ο μαθητής εισάγει την κλασματική παράσταση που θέλει να υπολογίσει και η εφαρμογή δίνει το τελικό αποτέλεσμα, τόσο σε κλασματική μορφή, όσο και ως δεκαδικό αριθμό. Επιπρόσθετα, ο μαθητής μπορεί να δει πολύ αναλυτικά όλα τα βήματα των υπολογισμών, ώστε να κατανοήσει τη διαδικασία. Μπορεί, επίσης, να επιλέξει αν θέλει να δει το τελικό αποτέλεσμα ως απλό κλάσμα ή ως μεικτό αριθμό (η μορφή του μεικτού αριθμού χρησιμοποιείται πολύ στο δημοτικό αλλά και στο γυμνάσιο).
Είναι διαθέσιμη δωρεάν στο Play Store και μπορείτε να την κατεβάσετε πατώντας εδώ.
Παρασκευή 1 Απριλίου 2022
Το παράδοξο του ψεύτη... Από τον Επιμενίδη στο Star Trek και ο γρίφος του γελωτοποιού
O Επιμενίδης από την Κρήτη (6ος αιώνας π.Χ.) ήταν θρησκευτικός διδάσκαλος, προφήτης και μάντης και είναι περισσότερο γνωστός για ένα λογικό παράδοξο που έχει συνδεθεί με το όνομά του. Η λέξη "παράδοξο" (παρά την δόξα) σημαίνει ό,τι είναι αντίθετο με την κοινή λογική, την καθιερωμένη άποψη και τη λογική συνέπεια. Ο Επιμενίδης, λοιπόν, έγραψε κάποτε:
"Οι Κρητικοί λένε πάντα ψέματα".
Αν σκεφτείτε καλά την παραπάνω πρόταση, θα δείτε ότι οδηγεί σε φαύλο κύκλο. Αν οι Κρητικοί λένε πάντα ψέματα, τότε και ο Επιμενίδης, ως Κρητικός λέει ψέματα. Άρα δεν αληθεύει η παραπάνω πρόταση, δηλαδή οι Κρητικοί δεν λένε πάντα ψέματα. Τότε όμως και ο Επιμενίδης δεν ψεύδεται κ.ο.κ.
Κάποιοι βέβαια θα σκεφτούν ότι το παράδοξο αυτό επιλύεται πολύ εύκολα, αφού στην προηγούμενη πρόταση κάνουμε μια εσφαλμένη γενίκευση. Στη ζωή του ένας άνθρωπος λέει και ψέματα και αλήθειες. Ποτέ όμως ταυτόχρονα. Δεν είναι δυνατόν όλοι οι Κρητικοί να λένε ψέματα και μάλιστα ταυτόχρονα...
Τα πράγματα, όμως, δεν είναι τόσο απλά, αφού δεν είναι αυτή η ουσία του παραδόξου. Ας ξεχάσουμε τους Κρητικούς και ας δούμε μια πρόταση, όπως οι κλασικές προτάσεις στα Μαθηματικά, που τις χειριζόμαστε με τη δίτιμη λογική των Μαθηματικών (και της Πληροφορικής), αληθής ή ψευδής:
"Αυτή η πρόταση είναι ψευδής".
Έστω ότι η παραπάνω πρόταση είναι αληθής. Τότε, σύμφωνα με αυτήν, είναι ψευδής.
Έστω ότι η παραπάνω πρόταση είναι ψευδής. Τότε, αφού δεν ισχύει αυτό που λέει, δηλαδή δεν είναι ψευδής, η πρόταση αυτή είναι αληθής. Τελικά τι είναι;
Η πρόταση αυτή είναι ταυτόχρονα αληθής και ψευδής. Το παράδοξο του Επιμενίδη ανήκει σε μια γενικότερη κατηγορία παραδόξων, τα λεγόμενα "παράδοξα του ψεύτη". Οι φιλόσοφοι χρησιμοποίησαν κατά καιρούς τα παράδοξα για να αντικρούσουν την πλάνη των αισθήσεων. Αντιθέτως, οι μαθηματικοί μάλλον τα αντιμετώπιζαν με τρόμο. Ήταν κάτι σαν το κουτί της Πανδώρας, που αν το ανοίξεις μπορεί να καταστραφεί όλο το μαθηματικό οικοδόμημα σε μια στιγμή! Τουλάχιστον αυτό ίσχυε μέχρι τα μέσα του 19ου αιώνα, οπότε και τα παράδοξα άρχισαν να αντιμετωπίζονται με τρόπο περισσότερο εποικοδομητικό.
Στο επεισόδιο "I, Mudd" του Star Trek - The Original Series (Season 2) γίνεται μια πετυχημένη αναφορά στο παράδοξο του ψεύτη. To πλήρωμα του Εντερπράιζ απάγεται και κρατείται σε έναν πλανήτη έξυπνων ανδροειδών. Με το τέχνασμα μιας έκρηξης, ο Κερκ και ο απατεώνας Χάρι Μαντ μπερδεύουν τον Νόρμαν, τον ηγέτη των ανδροειδών, χρησιμοποιώντας το παράδοξο του ψεύτη:
ΝΟΡΜΑΝ: Μα δεν υπήρξε έκρηξη...
ΜΑΝΤ: Είπα ψέματα.
ΝΟΡΜΑΝ: Τι;
ΚΕΡΚ: Είπε ψέματα. Όλα όσα σου λέει ο Χάρι είναι ψέματα. Να ξέρεις ότι όλα όσα σου λέει ο Χάρι είναι ένα ψέμα.
ΜΑΝΤ: Άκου με προσεκτικά, Νόρμαν. Σου λέω ψέματα.
ΝΟΡΜΑΝ: Λες ότι είσαι ψεύτης, αλλά αν ό,τι λες είναι ψέμα, τότε λες την αλήθεια, αλλά δεν μπορείς να πεις την αλήθεια, επειδή ό,τι λες είναι ψέματα. Λες ψέματα... Λες την αλήθεια... Αλλά δεν μπορείς να... Παράλογο! Παράλογο! Παρακαλώ εξηγήστε... Μόνο οι άνθρωποι μπορούν να το εξηγήσουν...
Επειδή ο Νόρμαν δεν μπορεί να επιλύσει το παράδοξο, το κεφάλι του αρχίζει να βγάζει καπνούς, ώσπου "μένει στον τόπο", αφήνοντας το πλήρωμα του Εντερπράιζ να δραπετεύσει.
Τέλος, ένας γρίφος λογικής που σχετίζεται με το σημερινό θέμα:
Ένας βασιλιάς, που είχε βαρεθεί το γελωτοποιό του και έψαχνε αφορμή να τον ξεφορτωθεί, τον κάλεσε και του είπε: "Πες κάτι, ό,τι θέλεις. Αν αυτό που θα πεις είναι ψέμα, θα σε κρεμάσω. Αν αυτό που θα πεις είναι αλήθεια, θα σε σφάξω". Ο γελωτοποιός στάθηκε για λίγο σκεπτικός και έπειτα είπε κάτι στον βασιλιά. Και έζησε!
Τι του είπε;;;
*~*-.-*~*-.-*~*
Αναπολιτάνος Διονύσιος, Εισαγωγή στη Φιλοσοφία των Μαθηματικών, Εκδόσεις Νεφέλη, 1961
Επιμενίδης - Βικιπαίδεια
Θαλής + φίλοι
Πέμπτη 24 Μαρτίου 2022
...and the Abel 2022 goes to...
Πηγή: The Abel Prize