Στην Άλγεβρα, μπορούμε με ένα οποιοδήποτε σύμβολο να συμβολίσουμε μια πράξη ή μια σειρά πράξεων που ορίσαμε μεταξύ δύο αριθμών. Αρκεί η πράξη αυτή να είναι καλά ορισμένη, δηλαδή το αποτέλεσμα της πράξης μεταξύ των δύο αριθμών να ορίζεται μονοσήμαντα και να ανήκει στο ίδιο σύνολο αριθμών με τους δύο αρχικούς.
Τετάρτη 29 Απριλίου 2020
Σάββατο 25 Απριλίου 2020
Κριτήρια Διαιρετότητας για τους αριθμούς από το 19 ως το 32!
Για να εξετάσουμε αν ένας ακέραιος αριθμός διαιρείται με το 19:
1. Διαγράφουμε το τελευταίο ψηφίο του αριθμού.
2. Στον αριθμό που προκύπτει προσθέτουμε 2 φορές το διαγραμμένο ψηφίο.
3. Αν το αποτέλεσμα (συμπεριλαμβανομένου του 0) διαιρείται με το 19, τότε και ο αρχικός αριθμός θα διαιρείται με το 19.
4. Αν δεν μπορούμε να αποφασίσουμε, επαναλαμβάνουμε τα τρία προηγούμενα βήματα μέχρι να προκύψει διψήφιος αριθμός.
π.χ. Θεωρούμε τον αριθμό 11.343
1. Διαγράφουμε το τελευταίο ψηφίο, δηλαδή το 3 και μένει ο αριθμός 1.134.
2. Στο 1.134 προσθέτουμε το διπλάσιο του 3, δηλαδή το 6:
1.134 + 2*3 = 1.134 + 6 = 1.140
3. Επειδή δεν μπορούμε να κρίνουμε αν ο αριθμός 1.140 διαιρείται με το 19, επαναλαμβάνουμε τα προηγούμενα βήματα:
1. Διαγράφουμε το τελευταίο ψηφίο του 1.140, δηλαδή το 0 και μένει ο αριθμός 114.
2. Στο 114 προσθέτουμε το διπλάσιο του 0, δηλαδή το 0:
114 + 2*0 = 114
3. Επαναλαμβάνουμε:
1. Διαγράφουμε το τελευταίο ψηφίο του 114 και μένει ο αριθμός 11.
2. Στο 11 προσθέτουμε το διπλάσιο του 4:
11 + 2*4 = 11 + 8 = 19
3. Το 19 διαιρείται με το 19, επομένως και ο αρχικός αριθμός διαιρείται με το 19.
π.χ. Θεωρούμε τον αριθμό 11.343
1. Διαγράφουμε το τελευταίο ψηφίο, δηλαδή το 3 και μένει ο αριθμός 1.134.
2. Στο 1.134 προσθέτουμε το διπλάσιο του 3, δηλαδή το 6:
1.134 + 2*3 = 1.134 + 6 = 1.140
3. Επειδή δεν μπορούμε να κρίνουμε αν ο αριθμός 1.140 διαιρείται με το 19, επαναλαμβάνουμε τα προηγούμενα βήματα:
1. Διαγράφουμε το τελευταίο ψηφίο του 1.140, δηλαδή το 0 και μένει ο αριθμός 114.
2. Στο 114 προσθέτουμε το διπλάσιο του 0, δηλαδή το 0:
114 + 2*0 = 114
3. Επαναλαμβάνουμε:
1. Διαγράφουμε το τελευταίο ψηφίο του 114 και μένει ο αριθμός 11.
2. Στο 11 προσθέτουμε το διπλάσιο του 4:
11 + 2*4 = 11 + 8 = 19
3. Το 19 διαιρείται με το 19, επομένως και ο αρχικός αριθμός διαιρείται με το 19.
Ένας ακέραιος αριθμός θα διαιρείται με το 20:
-Αν διαιρείται ταυτόχρονα και με το 4 και με το 5,
ή, συνδυάζοντας τα κριτήρια διαιρετότητας του 4 και του 5:
-Αν το τελευταίο του ψηφίο είναι 0 ή 5 και τα τελευταία δύο ψηφία του σχηματίζουν διψήφιο αριθμό που διαιρείται με το 4.
π.χ. Ο αριθμός 1.360 διαιρείται με το 20, γιατί:
-διαιρείται με το 4, αφού τελειώνει σε 60 και το 60 διαιρείται με το 4
και
-διαιρείται με το 5, αφού τελειώνει σε 0.
-Αν το τελευταίο του ψηφίο είναι 0 ή 5 και τα τελευταία δύο ψηφία του σχηματίζουν διψήφιο αριθμό που διαιρείται με το 4.
π.χ. Ο αριθμός 1.360 διαιρείται με το 20, γιατί:
-διαιρείται με το 4, αφού τελειώνει σε 60 και το 60 διαιρείται με το 4
και
-διαιρείται με το 5, αφού τελειώνει σε 0.
Ένας ακέραιος αριθμός θα διαιρείται με το 21:
Αν διαιρείται ταυτόχρονα και με το 3 και με το 7,
δηλαδή αν ικανοποιεί ταυτόχρονα τα κριτήρια διαιρετότητας του 3 και του 7.
π.χ. Θεωρούμε τον αριθμό 273.
-Διαιρείται με το 3, αφού το άθροισμα των ψηφίων του είναι 2 + 7 + 3 = 12 και το 12 διαιρείται με το 3.
-Διαιρείται με το 7. Πράγματι, 27 - 2*3 = 21 και το 21 διαιρείται με το 7.
Οπότε ο αριθμός 273 διαιρείται με το 21.
Ένας ακέραιος αριθμός θα διαιρείται με το 22:
Αν διαιρείται ταυτόχρονα και με το 2 και με το 11,
δηλαδή αν ικανοποιεί ταυτόχρονα τα κριτήρια διαιρετότητας του 2 και του 11.
π.χ. Θεωρούμε τον αριθμό 1.166.
-Διαιρείται με το 2, αφού τελειώνει σε 6, είναι δηλαδή άρτιος αριθμός.
-Διαιρείται με το 11.
Πράγματι, το άθροισμα των ψηφίων που βρίσκονται στις περιττές θέσεις είναι 1 + 6 = 7.
Το άθροισμα των ψηφίων που βρίσκονται στις περιττές θέσεις είναι 1 + 6 = 7.
Η διαφορά των δύο αθροισμάτων είναι 7 - 7 = 0.
Σύμφωνα με το κριτήριο διαιρετότητας του 11, ο αριθμός 1.166 διαιρείται με το 11.
Άρα τελικά ο αριθμός 1.166 διαιρείται με το 22.
Για να εξετάσουμε αν ένας ακέραιος αριθμός διαιρείται με το 23:
1. Διαγράφουμε το τελευταίο ψηφίο του αριθμού.
2. Στον αριθμό που προκύπτει προσθέτουμε 7 φορές το διαγραμμένο ψηφίο.
4. Αν ο αριθμός που προκύπτει διαιρείται με το 23 (δηλαδή αν προκύψει 23, 46, 69 ή 92), τότε και ο αρχικός αριθμός διαιρείται με το 23.
π.χ. Θεωρούμε τον αριθμό 35.949.
1. Διαγράφουμε το τελευταίο ψηφίο, δηλαδή το 9 και μένει ο αριθμός 3.594.
2. Στο 3.594 προσθέτουμε το επταπλάσιο του 9:
3.594 + 7*9 = 3.594 + 63 = 3.657
3. Επαναλαμβάνουμε τα δύο προηγούμενα βήματα:
1. Διαγράφουμε το τελευταίο ψηφίο, δηλαδή το 7 και μένει ο αριθμός 365.
2. Στο 365 προσθέτουμε το επταπλάσιο του 7:
365 + 7*7 = 365 + 49 = 414
3. Επαναλαμβάνουμε τα δύο προηγούμενα βήματα:
1. Διαγράφουμε το τελευταίο ψηφίο, δηλαδή το 4 και μένει ο αριθμός 41.
2. Στο 41 προσθέτουμε το επταπλάσιο του 4:
41 + 7*4 = 41 + 28 = 69
3. Το 69 διαιρείται με το 23, άρα και ο αρχικός αριθμός διαιρείται με το 23.
Ένας ακέραιος αριθμός θα διαιρείται με το 24:
Αν διαιρείται ταυτόχρονα και με το 3 και με το 8,
δηλαδή αν ικανοποιεί ταυτόχρονα τα κριτήρια διαιρετότητας του 3 και του 8.
π.χ. Θεωρούμε τον αριθμό 768.
-Διαιρείται με το 3, αφού το άθροισμα των ψηφίων του είναι 7 + 6 + 8 = 21 και το 21 διαιρείται με το 3.
-Διαιρείται με το 8, αφού το ψηφίο των εκατοντάδων (7) είναι περιττός αριθμός και τα τελευταία δύο ψηφία συν 4, σχηματίζουν τον αριθμό 68 + 4 = 72, ο οποίος διαιρείται με το 8.
Ένας ακέραιος αριθμός θα διαιρείται με το 25, αν τα τελευταία δύο ψηφία του σχηματίζουν διψήφιο αριθμό που διαιρείται με το 25,
δηλαδή αν τα δύο τελευταία ψηφία του είναι:
00 ή 25 ή 50 ή 75.
π.χ. Ο αριθμός 12.600 διαιρείται με το 25, αφού τελειώνει σε 00.
Ένας ακέραιος αριθμός θα διαιρείται με το 24,
αν διαιρείται ταυτόχρονα και με το 2 και με το 13,
π.χ. Θεωρούμε τον αριθμό 832.
-Διαιρείται με το 2, αφού τελειώνει σε 2, είναι δηλαδή άρτιος αριθμός.
-Διαιρείται με το 13.
Πράγματι, 83 - 9*2 = 83 - 18 = 65 και το 65 διαιρείται με το 13.
Άρα ο αριθμός 832 διαιρείται με το 26.
Για να κρίνουμε αν ένας ακέραιος αριθμός διαιρείται με το 27, αρχικά εξετάζουμε το πλήθος των ψηφίων του.
1η περίπτωση: Αν ο αριθμός είναι τριψήφιος, τότε:
1. Διαγράφουμε το ψηφίο των εκατοντάδων (το πρώτο ψηφίο).
2. Από τον διψήφιο αριθμό που μένει, αφαιρούμε το 8πλάσιο του ψηφίου που έχουμε διαγράψει.
3. Αν ο αριθμός που προκύψει διαιρείται με το 27 (συμπεριλαμβανομένων του 0 αλλά και αρνητικών αριθμών), τότε και ο αρχικός αριθμός διαιρείται με το 27.
2η περίπτωση: Αν ο αριθμός έχει τουλάχιστον 4 ψηφία, τότε:
1. Διαγράφουμε τα τελευταία τρία ψηφία του, τα οποία αποτελούν έναν τριψήφιο αριθμό.
2. Στον αριθμό που μένει, προσθέτουμε τον τριψήφιο αριθμό από το βήμα 1.
3. Το άθροισμα σαφώς θα είναι ένας αριθμός μικρότερος από τον αρχικό. Συνεχίζουμε τα βήματα 1 και 2, μέχρι να προκύψει τριψήφιος αριθμός.
4. Ακολουθούμε τα βήματα όπως περιγράφονται στην 1η περίπτωση.
π.χ. Θεωρούμε τον αριθμό 1.242
Είναι 4ψήφιος, άρα ακολουθούμε τα βήματα της 2ης περίπτωσης:
1. Διαγράφουμε τα τελευταία τρία ψηφία του, δηλαδή τον αριθμό 242.
2. Στον αριθμό που έμεινε, δηλαδή το 1, προσθέτουμε το 242.
1 + 242 = 243.
3. Προέκυψε 3ψήφιος αριθμός, άρα ακολουθούμε τα βήματα της 1ης περίπτωσης:
1. Από τον αριθμό 243, διαγράφουμε το ψηφίο των εκατοντάδων, δηλαδή το 2.
2. Από τον αριθμό που μένει, δηλαδή το 43, αφαιρούμε το 8πλάσιο του 2:
43 - 8*2 = 43 - 16 = 27
3. Προκύπτει ο αριθμός 27, ο οποίος προφανώς διαιρείται με το 27. Άρα και ο αρχικός αριθμός διαιρείται με το 27.
Ένας ακέραιος αριθμός θα διαιρείται με το 28,
αν διαιρείται ταυτόχρονα και με το 4 και με το 7,
π.χ. Θεωρούμε τον αριθμό 224.
-Διαιρείται με το 4, αφού τα δύο τελευταία ψηφία του σχηματίζουν τον αριθμό 24, ο οποίος διαιρείται με το 4.
-Διαιρείται με το 7. Πράγματι:
22 - 2*4 = 22 - 8 = 14
Το 14 διαιρείται με το 7, άρα και ο αρχικός αριθμός διαιρείται με το 7.
Οπότε διαιρείται και με το 28.
Για να εξετάσουμε αν ένας ακέραιος αριθμός διαιρείται με το 29:
1. Διαγράφουμε το τελευταίο ψηφίο του αριθμού.
2. Στον αριθμό που προκύπτει προσθέτουμε 3 φορές το διαγραμμένο ψηφίο.
4. Αν ο αριθμός που προκύπτει διαιρείται με το 29, τότε και ο αρχικός αριθμός διαιρείται με το 29.
π.χ. Θεωρούμε τον αριθμό 1.914.
1. Διαγράφουμε το τελευταίο ψηφίο, δηλαδή το 4 και μένει ο αριθμός 191.
2. Στο 191 προσθέτουμε το τριπλάσιο του 4:
191 + 3*4 = 191 + 12 = 203
3. Επαναλαμβάνουμε για τον αριθμό 203 τα δύο προηγούμενα βήματα:
1. Διαγράφουμε το τελευταίο ψηφίο, δηλαδή το 3 και μένει ο αριθμός 20.
2. Στο 20 προσθέτουμε το τριπλάσιο του 3:
20 + 3*3 = 20 + 9 = 29
3. Το 29 προφανώς διαιρείται με το 29, άρα και ο αρχικός αριθμός, το 1.914 διαιρείται με το 29.
Ένας ακέραιος αριθμός θα διαιρείται με το 30
αν το τελευταίο του ψηφίο είναι το 0 και το άθροισμα των ψηφίων του είναι αριθμός που διαιρείται με το 3
αν το τελευταίο του ψηφίο είναι το 0 και το άθροισμα των ψηφίων του είναι αριθμός που διαιρείται με το 3
(δηλαδή αν διαιρείται ταυτόχρονα και με το 3 και με το 10).
π.χ. Θεωρούμε τον αριθμό 1.950.
-Το τελευταίο του ψηφίο είναι το 0, δηλαδή διαιρείται με το 10.
-Το άθροισμα των ψηφίων του είναι
1 + 9 + 5 + 0 = 15
και το 15 διαιρείται με το 3, άρα ο αριθμός 1.950 διαιρείται με το 3.
Επομένως ο αριθμός 1.950 διαιρείται με το 30.
Για να εξετάσουμε αν ένας ακέραιος αριθμός διαιρείται με το 31:
1. Διαγράφουμε το τελευταίο ψηφίο του αριθμού.
2. Από τον αριθμό που προκύπτει αφαιρούμε 3 φορές το διαγραμμένο ψηφίο.
4. Αν ο αριθμός που προκύπτει διαιρείται με το 31, τότε και ο αρχικός αριθμός διαιρείται με το 31.
π.χ. Θεωρούμε τον αριθμό 775.
1. Διαγράφουμε το τελευταίο ψηφίο του 775, δηλαδή το 5 και μένει ο αριθμός 77.
2. Από το 77 αφαιρούμε το τριπλάσιο του 5:
77 - 3*5 = 77 - 15 = 62
3. Το 62 διαιρείται με το 31, άρα και ο αρχικός αριθμός, το 775 διαιρείται με το 31.
Για να εξετάσουμε αν ένας ακέραιος αριθμός διαιρείται με το 32:
-Αν ο αριθμός έχει περισσότερα από 5 ψηφία, τότε: Ο αριθμός διαιρείται με το 32 αν τα τελευταία 5 ψηφία του σχηματίζουν αριθμό που διαιρείται με το 32.
-Και πώς θα ελέγξουμε αν ένας πενταψήφιος αριθμός διαιρείται με το 32;;;
1. Απομονώνουμε τα δύο τελευταία ψηφία του αριθμού.
π.χ. Θεωρούμε τον αριθμό 1.088.256
-Αρκεί να απομονώσουμε τα τελευταία πέντε ψηφία του και να ελέγξουμε αν ο αριθμός 88.256 διαιρείται με το 32.
-Ελέγχουμε το ψηφίο στη θέση των Δεκάδων Χιλιάδων. Το 8 είναι άρτιος αριθμός, άρα αρκεί να ελέγξουμε αν τα τελευταία τέσσερα ψηφία του, δηλαδή ο αριθμός 8.256 διαιρείται με το 32.
-Από τον αριθμό 8.256 διαγράφουμε τα δύο τελευταία του ψηφία (το 56).
-Προσθέτουμε το 56 στο 4πλάσιο του αριθμού που απέμεινε, δηλαδή στο 4πλάσιο του 82:
4*82 + 56 = 384
Αρκεί να εξετάσουμε τώρα αν το 384 διαιρείται με το 32.
-Επαναλαμβάνουμε τα προηγούμενα βήματα:
-Από τον αριθμό 384 διαγράφουμε τα δύο τελευταία του ψηφία (το 84).
-Προσθέτουμε το 84 στο 4πλάσιο του αριθμού που απέμεινε, δηλαδή στο 4πλάσιο του 3:
4*3 + 84 = 96
-Το 96 διαιρείται με το 32 (είναι 96=3*32) άρα και ο αρχικός αριθμός, το 1.088.256 διαιρείται με το 32.
- Αν το ψηφίο στη θέση των Δεκάδων Χιλιάδων (το πρώτο ψηφίο) είναι άρτιος αριθμός, αρκεί να ελέγξουμε αν τα τελευταία τέσσερα ψηφία σχηματίζουν αριθμό που διαιρείται με το 32.
- Αν το ψηφίο στη θέση των Δεκάδων Χιλιάδων (το πρώτο ψηφίο) είναι περιττός αριθμός, αρκεί να ελέγξουμε αν τα τελευταία τέσσερα ψηφία του συν 16, σχηματίζουν αριθμό που διαιρείται με το 16.
-Μόλις προκύψει τριψήφιος ή τετραψήφιος αριθμός, για να ελέγξουμε αν διαιρείται με το 32, ακολουθούμε το εξής κριτήριο:
1. Απομονώνουμε τα δύο τελευταία ψηφία του αριθμού.
2. Προσθέτουμε τον διψήφιο αριθμό στο 4πλάσιο του αριθμού που απέμεινε.
3. Αν ο αριθμός που προκύψει διαιρείται με το 32, τότε και ο αρχικός αριθμός διαιρείται με το 32.
π.χ. Θεωρούμε τον αριθμό 1.088.256
-Αρκεί να απομονώσουμε τα τελευταία πέντε ψηφία του και να ελέγξουμε αν ο αριθμός 88.256 διαιρείται με το 32.
-Ελέγχουμε το ψηφίο στη θέση των Δεκάδων Χιλιάδων. Το 8 είναι άρτιος αριθμός, άρα αρκεί να ελέγξουμε αν τα τελευταία τέσσερα ψηφία του, δηλαδή ο αριθμός 8.256 διαιρείται με το 32.
-Από τον αριθμό 8.256 διαγράφουμε τα δύο τελευταία του ψηφία (το 56).
-Προσθέτουμε το 56 στο 4πλάσιο του αριθμού που απέμεινε, δηλαδή στο 4πλάσιο του 82:
4*82 + 56 = 384
Αρκεί να εξετάσουμε τώρα αν το 384 διαιρείται με το 32.
-Επαναλαμβάνουμε τα προηγούμενα βήματα:
-Από τον αριθμό 384 διαγράφουμε τα δύο τελευταία του ψηφία (το 84).
-Προσθέτουμε το 84 στο 4πλάσιο του αριθμού που απέμεινε, δηλαδή στο 4πλάσιο του 3:
4*3 + 84 = 96
-Το 96 διαιρείται με το 32 (είναι 96=3*32) άρα και ο αρχικός αριθμός, το 1.088.256 διαιρείται με το 32.
Τετάρτη 22 Απριλίου 2020
Οι δέκα εντολές του George Polya προς τον δάσκαλο των Μαθηματικών
O George Polya συνέβαλε δραστικά στην ενίσχυση της σύνδεσης ανάμεσα στα Μαθηματικά και τη Διδακτική, αλλά και ανάμεσα στους μαθηματικούς και στους καθηγητές των Μαθηματικών. Στο βιβλίο του "Mathematical Discovery on Undestanding, Learning and Teaching Problem Solving" δίνει τις δέκα εντολές προς όσους διδάσκουν Μαθηματικά:
I. Να ενδιαφέρεσαι για το αντικείμενό σου.
II. Να γνωρίζεις το αντικείμενό σου.
III. Να γνωρίζεις τους τρόπους μάθησης: Ο καλύτερος τρόπος για να μάθεις κάτι είναι να το ανακαλύψεις μόνος σου.
IV. Προσπάθησε να διαβάζεις τα πρόσωπα των μαθητών σου, προσπάθησε να δεις τις προσδοκίες και τις δυσκολίες τους, τοποθέτησε τον εαυτό σου στη θέση τους.
V. Δώσε στους μαθητές σου, όχι μόνο πληροφορία, αλλά και καθοδήγηση χειρισμού της πληροφορίας, τρόπους σκέψης, τη συνήθεια της μεθοδικής εργασίας.
VI. Άφησέ τους να μάθουν να κάνουν νοερές εκτιμήσεις.
VII. Άφησέ τους να μάθουν να αποδεικνύουν.
VIII. Να επισημαίνεις στα παρόντα προβλήματα εκείνα τα χαρακτηριστικά που μπορεί να φανούν χρήσιμα στην επίλυση μελλοντικών προβλημάτων - προσπάθησε να αποκαλύψεις το γενικό μοτίβο που κρύβεται πίσω από την παρούσα συγκεκριμένη κατάσταση.
IX. Μην χαρίζεις ολόκληρο το μυστικό σου μονομιάς -άσε τους μαθητές σου να μαντέψουν προτού το πεις- άφησέ τους να το ανακαλύψουν μόνοι τους, όσο είναι εφικτό.
X. Πρότεινε την πληροφορία, μην τους βάζεις να την καταπιούν με το ζόρι.
Πηγή: Mathematics for Teaching
Κυριακή 19 Απριλίου 2020
Πασχαλινός γρίφος!
Καλό Πάσχα σε όλους! Φέτος, εξαιτίας του COVID-19 δεν κάναμε Πάσχα στο χωριό μαζί με όλους τους συγγενείς...
Το περασμένο Πάσχα όμως, είχαν μαζευτεί κάμποσοι συγγενείς γύρω από το γιορτινό τραπέζι στο χωριό. Αν γνωρίζετε ότι μεταξύ των συγγενών έγιναν 190 τσουγκρίσματα αυγών και κάθε ένας τσούγκρισε το αυγό του ακριβώς μια φορά με κάθε άλλον, να βρείτε πόσοι συγγενείς είχαν μαζευτεί.
Τρίτη 14 Απριλίου 2020
Τα καλύτερα μαθηματικά ανέκδοτα
Άπειροι μαθηματικοί μπαίνουν σ' ένα μπαρ. Ο πρώτος λέει: "Θα πάρω μια μπύρα". Ο δεύτερος λέει: "Θα πάρω μισή μπύρα". Ο τρίτος λέει: "Θα πάρω ένα τέταρτο της μπύρας". Ο τέταρτος λέει: "Θα πάρω τη μισή μπύρα απ' όση ζήτησε ο προηγούμενος" και ούτω καθεξής... Οπότε ο μπάρμαν χωρίς να χάσει χρόνο βγάζει ακριβώς δύο ποτήρια μπύρα. "Πώς; Μόνο δύο ποτήρια μπύρα για όλους εμάς;", διαμαρτύρονται οι μαθηματικοί. "Ελάτε τώρα παιδιά", τους λέει ο μπάρμαν. "Πρέπει να ξέρετε τα όριά σας!"
Ένας μηχανικός, ένας φυσικός κι ένας μαθηματικός διανυκτερεύουν σ' ένα ξενοδοχείο. Κατά τη διάρκεια της νύχτας, ξεσπά φωτιά έξω από το δωμάτιο του μηχανικού. Ο μηχανικός ξυπνά μυρίζοντας τον καπνό, βγαίνει στο διάδρομο και βλέπει φωτιά! Γεμίζει λοιπόν το καλάθι των σκουπιδιών από το δωμάτιό του με νερό και έτσι σβήνει τη φωτιά. Πάει ήσυχος για ύπνο. Αργότερα ξεσπά φωτιά έξω από το δωμάτιο του φυσικού. Ο φυσικός ξυπνά μυρίζοντας τον καπνό, βγαίνει στο διάδρομο και βλέπει φωτιά! Παίρνει λοιπόν από το τέλος του διαδρόμου την πυροσβεστική μάνικα που υπήρχε και, αφού υπολόγισε την κατεύθυνση της φωτιάς, την απόστασή του από τη φωτιά και την πίεση του νερού, καταφέρνει να σβήσει τη φωτιά με την ελάχιστη απαιτούμενη ποσότητα νερού και ενέργειας. Πάει ήσυχος για ύπνο. Αργότερα ξεσπά φωτιά έξω από το δωμάτιο του μαθηματικού. Ο μαθηματικός ξυπνά μυρίζοντας τον καπνό, βγαίνει στο διάδρομο και βλέπει φωτιά! Αμέσως εντοπίζει έναν πυροσβεστήρα στην άκρη του διαδρόμου. "Α, ώστε υπάρχει τουλάχιστον μία λύση στο πρόβλημα", σκέφτεται και πάει ήσυχος για ύπνο.
-Γιατί μια κότα διέσχισε την ταινία του Möbius;
-Για να βρεθεί στην ίδια πλευρά!
-Γιατί η ταινία του Möbius δεν μπόρεσε να γραφτεί στο Γενικό Λύκειο;
-Έπρεπε να επιλέξει προσανατολισμό!
-Πώς μπορείς να κάνεις εύκολα πράξεις με το μυαλό;
-Χρησιμοποίησε φανταστικούς αριθμούς!
-Σε πόση ώρα υπολογίζει ένας μαθηματικός ένα άθροισμα αρρήτων;
-Στο π+φ!-Πώς μαλώνει ένας μαθηματικός τα παιδιά του;
-Σου το είπα ν φορές, σου το είπα ν+1 φορές...Αμάν πια!
-Πώς βρίζει ένας μαθηματικός;
-Πόσοι μαθηματικοί χρειάζονται για ν' αλλάξουν μια λάμπα;
-Τρεις... Ένας για να αποδείξει την ύπαρξη, ένας τη μοναδικότητα κι ένας για να κατασκευάσει τον αλγόριθμο αλλαγής λάμπας.
-Γιατί οι άθεοι δεν μπορούν να λύσουν πολυωνυμικές εξισώσεις βαθμού μεγαλύτερου του 1;
-Επειδή δεν πιστεύουν σε ανώτερες δυνάμεις...
-Τι είναι κίτρινο και πλήρες;
-Ένας Χώρος Bananach!
-Γιατί η Κοκκινοσκουφίτσα μελετά Γενική Τοπολογία;
-Για να μη χάνεται στα μονοπάτια!
-Τι είναι το βούτυρο για το ψωμί;
-Χώρος επικάλυψης.
-Πώς λέγεται η Τοπολογία που έχει πυρετό;
-Ασθενής Τοπολογία.
-Ποιο είναι το πιο σύντομο μαθηματικό ανέκδοτο;
-Έστω ε<0.
Κυριακή 5 Απριλίου 2020
Τα Μαθηματικά στην Τέχνη: Σφαίρα και σφαιρικά πολύεδρα
ΣΦΑΙΡΑ
Τα βιβλία γράφουν...
Σφαίρα είναι το σχήμα που παράγεται από την περιστροφή ενός κύκλου (Ο, ρ) με άξονα περιστροφής μια διάμετρό του.
Τα βιβλία επίσης γράφουν...
Σφαίρα είναι το σύνολο των σημείων Μ του χώρου που απέχουν από ένα σταθερό σημείο Ο σταθερή απόσταση ρ, δηλαδή ισχύει:
ΟΜ = ρ.
Τα βιβλία γράφουν...
Σφαίρα είναι το σχήμα που παράγεται από την περιστροφή ενός κύκλου (Ο, ρ) με άξονα περιστροφής μια διάμετρό του.
Τα βιβλία επίσης γράφουν...
Σφαίρα είναι το σύνολο των σημείων Μ του χώρου που απέχουν από ένα σταθερό σημείο Ο σταθερή απόσταση ρ, δηλαδή ισχύει:
ΟΜ = ρ.
 |
| Rene Magritte (1898 - 1967) |
 |
| Rene Magritte (1898 - 1967) - "L'ombre Monumentale" (1932) |
 |
| Ivan Kliun (1873- 1943) - "Σφαιρική μη αντικειμενική σύνθεση" (1922-25) |
 |
| A.J. Edwards (Σύγχρονος καλλιτέχνης) - "Game Room" |
 |
| Barbara Fox (Σύγχρονη ζωγράφος) - "Billiard Balls - Still Life" |
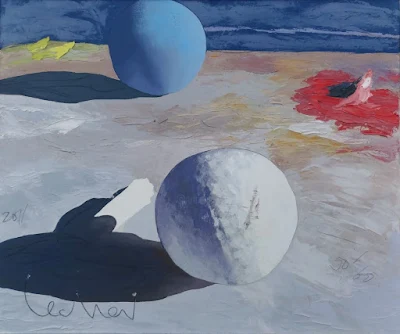 |
| Georgi Lechev (Σύγχρονος καλλιτέχνης) - "Dialog Between White and Blue" (2011) |
 |
| Allen Donnelly (Σύγχρονος καλλιτέχνης και συγγραφέας) - "On the beach" |
 |
| James Pikerton (σύγχρονος ζωγράφος) - "Shadow Spheres" (2015) |
 |
| James Pikerton (σύγχρονος ζωγράφος) - "Sphere Orb" |
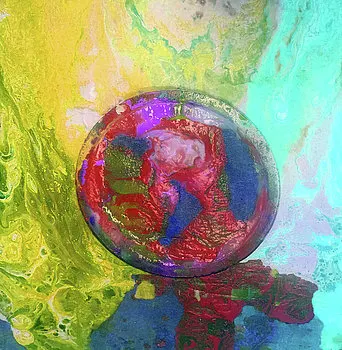 |
| James Pikerton (σύγχρονος ζωγράφος) - "Red Sphere" |
 |
| Katie Morris (Σύγχρονη ζωγράφος και καθηγήτρια καλλιτεχνικών) - "Sports Spheres" |
 |
| Katie Morris (Σύγχρονη ζωγράφος και καθηγήτρια καλλιτεχνικών) - "Sports Spheres" |
 |
| Katie Morris (Σύγχρονη ζωγράφος και καθηγήτρια καλλιτεχνικών) - "Sports Spheres" |
 |
| Katie Morris (Σύγχρονη ζωγράφος και καθηγήτρια καλλιτεχνικών) - "Sports Spheres" |
 |
| Katie Morris (Σύγχρονη ζωγράφος και καθηγήτρια καλλιτεχνικών) - "Sports Spheres" |
 |
| Russell Kightley (Σύγχρονος καλλιτέχνης) - "Sphere Equations" |
Τι γίνεται όταν επιτρέψουμε στα πολύεδρα να έχουν καμπυλωτές ακμές και έδρες;
ΣΦΑΙΡΙΚΑ ΠΟΛΥΕΔΡΑ
Τα βιβλία γράφουν...
Η επιφάνεια της σφαίρας μπορεί να χωριστεί με ευθύγραμμα τμήματα σε οριοθετούμενες περιοχές, για να σχηματίσει ένα σφαιρικό πολύεδρο. Μεγάλο μέρος της θεωρίας των συμμετρικών πολυέδρων προκύπτει ευκολότερα με αυτόν τον τρόπο. Τα σφαιρικά πολύεδρα έχουν μια μακρά και αξιοσέβαστη ιστορία. Ο Poinsot, χρησιμοποιώντας σφαιρικά πολύεδρα, ανακάλυψε τα τέσσερα κανονικά αστεροειδή πολύεδρα. Τα πρώτα πολύεδρα που κατασκεύασε ο άνθρωπος ήταν σφαιρικά πολύεδρα σκαλισμένα σε πέτρα.
 |
| Paolo Uccello (1397 - 1475) - "Γεωμετρική Σφαίρα" |
 |
| Martino da Udine (1470 - 1548) - Σπουδή στη Γεωμετρία και στην προοπτική |
.*.〰.*.〰.*.〰.*.〰.*.〰.*.〰.*.
"Μεταχειρίσου τη φύση μέσω του κυλίνδρου, της σφαίρας και του κώνου, όλα τοποθετημένα με προοπτική, ώστε κάθε πλευρά ενός αντικειμένου ή ενός επιπέδου να κατευθύνεται προς ένα κεντρικό σημείο. Αν μάθουμε να βασίζουμε τη ζωγραφική μας πάνω σ' αυτά τα απλά σχήματα, θα μπορέσουμε να πετύχουμε τα πάντα".
Paul Cezanne (1839 - 1906)
.*.〰.*.〰.*.〰.*.〰.*.〰.*.〰.*.
Πηγές:
- Ευκλείδεια Γεωμετρία Α' και Β' Γενικού Λυκείου, Ινστιτούτο Τεχνολογίας Υπολογιστών και Εκδόσεων "Διόφαντος", 2015
- H.L.C Jaffe, Η ζωγραφική στον 20ό αιώνα, Εκδόσεις Νεφέλη, 1984
- Adventures of an art teacher by Katie Morris
- Allen Donnelly
- Fine Art America: James Pikerton
- Pixels: Russell Kightley
- Wolfram Math World: Sphere
- wikipedia.org
Τετάρτη 1 Απριλίου 2020
Γρίφος: Ο βαρόνος Μινχάουζεν και το κυνήγι της πάπιας
Επί πολλά χρόνια, ο βαρόνος Μινχάουζεν πήγαινε καθημερινά στη λίμνη για να κυνηγήσει πάπιες. Την 1η Αυγούστου του 1896, είπε στον μάγειρά του: "Σήμερα πέτυχα περισσότερες πάπιες απ' ό,τι προχθές, αλλά λιγότερες από όσες την ίδια ημέρα την προηγούμενη εβδομάδα". Επί πόσες μέρες μπορεί να ισχυρίζεται ο βαρόνος αυτό το πράγμα;
(Σημειώστε ότι εδώ ο βαρόνος Μινχάουζεν δε λέει ψέματα!!!)
Εγγραφή σε:
Σχόλια (Atom)





















