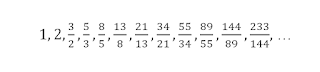Πώς οι αρχαίοι Έλληνες διαμόρφωσαν τα σύγχρονα μαθηματικά

Πριν από περίπου 2.500 χρόνια, μια ομάδα Ελλήνων με επαναστατικό τρόπο σκέψης διαμόρφωσε την αντίληψη που έχουμε σήμερα για τα μαθηματικά, μέσα από την ιδέα της μαθηματικής απόδειξης. Στο σύντομο animated βίντεο που δημοσίευσε το Royal Institution, παρουσιάζεται πώς οι αρχαίοι Έλληνες χρησιμοποίησαν τα μαθηματικά, όχι απλώς για να κάνουν υπολογισμούς, αλλά με σκοπό να ερμηνεύσουν τον κόσμο.

"Ο Αρχιμήδης θα μνημονεύεται όταν ο Αισχύλος θα έχει ξεχαστεί, γιατί οι γλώσσες πεθαίνουν, ενώ οι μαθηματικές ιδέες είναι αθάνατες. Ίσως η αθανασία είναι μια ανόητη λέξη, αλλά μάλλον ο μαθηματικός έχει την καλύτερη τύχη, ό,τι κι αν αυτό σημαίνει".

(G. H. Hardy)

1/6/2018: Παγκόσμια ημέρα του χρυσού αριθμού «φ»... (Μέρος 1º - Γνωριμία με τον αριθμό «φ»)

Τι κοινό έχουν οι ζωγραφικοί πίνακες της Αναγέννησης, το κουνουπίδι, η αναπαραγωγή των κουνελιών και μια πιστωτική κάρτα; Η απάντηση είναι ο αριθμός 1,61803398874989484..., ο "χρυσός αριθμός", ή "χρυσή αναλογία". Τα δεκαδικά του ψηφία είναι άπειρα και η ακολουθία τους δεν επαναλαμβάνεται. Μάθετε τι τον καθιστά τόσο μαγικό!

Όπως ο π (3,14) εκφράζει το πιο τέλειο γεωμετρικό σχήμα, τη σφαίρα, έτσι και ο φ (1,618) είναι ο αριθμός της «ομορφιάς». Ο μοναχός του 15^ου αιώνα Luca Pacioli, επηρεασμένος από την αντίληψη της εποχής ότι οι νέες γνώσεις της επιστήμης έπρεπε να ενταχθούν στο εκκλησιαστικό δόγμα, τον ονόμασε «Θεία Αναλογία» («Divina Proportione»). Ο Leonardo DaVinci τον ονόμασε «Χρυσό Αριθμό». Αιώνες αργότερα, ο μαθηματικός Mark Barr θα τον συμβόλιζε με το ελληνικό γράμμα φ, προς τιμήν του γλύπτη Φειδία, ο οποίος ήταν από τους πρώτους που δημιουργούσαν έργα με βάση τον αριθμό αυτό.

ΤΑ ΕΥΘΥΓΡΑΜΜΑ ΤΜΗΜΑΤΑ ΤΟΥ ΕΥΚΛΕΙΔΗ

Η αφετηρία είναι γεωμετρική. Ο Ευκλείδης στα «Στοιχεία» έδωσε τον πρώτο γραπτό ορισμό της χρυσής τομής, την οποία ονόμασε «άκρος και μέσος λόγος».

Ο Ευκλείδης παίρνει ένα ευθύγραμμο τμήμα και το διαιρεί σε δύο τμήματα. Η χρυσή τομή είναι εκείνο το σημείο που χωρίζει το ευθύγραμμο τμήμα στα δυο τμήματα a, b, έτσι ώστε  ο λόγος του αθροίσματος τους a+b προς τη μεγαλύτερη ποσότητα είναι ίσος με το λόγο της μεγαλύτερης ποσότητας προς τη μικρότερη.

Ο λόγος αυτός λέγεται «χρυσός λόγος» και σύμφωνα με τον ορισμό του Ευκλείδη, υπολογίζεται ότι έχει αριθμητική τιμή 1,618..., δηλαδή ότι το μεγαλύτερο τμήμα θα έχει πάντα 1,618... φορές μεγαλύτερο μήκος από το μικρότερο. 

ΧΡΥΣΟ ΟΡΘΟΓΩΝΙΟ ΚΑΙ ΧΡΥΣΗ ΕΛΙΚΑ

Ένα ορθογώνιο παραλληλόγραμμο λέγεται «χρυσό», όταν το πηλίκο της μεγαλύτερης προς τη μικρότερη πλευρά του ισούται με φ. 

Αυτό το ορθογώνιο έχει μια ιδιότητα που το ξεχωρίζει από όλα τα άλλα: αν αφαιρέσουμε από τη μια πλευρά το μεγαλύτερο δυνατό τετράγωνο, απομένει ένα καινούργιο ορθογώνιο, που είναι επίσης χρυσό, και αυτό μπορεί να συνεχιστεί επ’ άπειρον. 

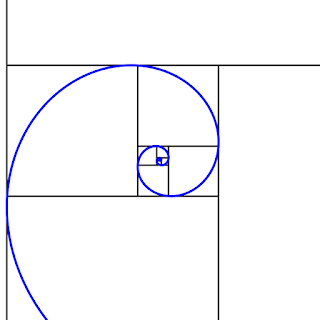
Αν ενώσει κανείς με μια καμπύλη τις κορυφές όλων αυτών των ορθογωνίων, που είναι και χρυσές τομές, σχηματίζεται μια λογαριθμική έλικα, η «χρυσή έλικα».

Αν θέλει κανείς να δει ένα χρυσό ορθογώνιο αρκεί να κοιτάξει μια πιστωτική κάρτα, το σχήμα της οποίας είναι ακριβώς αυτό. 

ΧΡΥΣΟ ΤΡΙΓΩΝΟ

Χρυσό λέγεται κάθε ισοσκελές  τρίγωνο στο οποίο ο λόγος της μεγάλης πλευράς προς τη μικρή θα είναι ίσος με φ. Κάθε ισοσκελές με γωνία κορυφής 36˚ είναι χρυσό.

ΤΟ ΣΥΜΒΟΛΟ ΤΩΝ ΠΥΘΑΓΟΡΕΙΩΝ

Η χρυσή αναλογία ήταν γνωστή στους Πυθαγορείους. Το σύμβολο της αδελφότητας των Πυθαγορείων ήταν το «πεντάγραμμο» ή «πεντάλφα», το αστέρι δηλαδή που σχηματίζεται από τις πέντε διαγωνίους του κανονικού πενταγώνου. Η χρυσή αναλογία εμφανίζεται στις πλευρές του αστεριού. 

Αποδεικνύεται ότι κάθε πλευρά του «πενταγράμμου» διαιρεί τις δύο άλλες σε χρυσή τομή.

Ακόμη, το πηλίκο του εμβαδού του κανονικού πενταγώνου με κορυφές τις άκρες της πεντάλφα προς το εμβαδόν του κανονικού πενταγώνου που σχηματίζεται εντός του αστεριού ισούται με φ.

ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΗΣ ΑΝΑΠΑΡΑΓΩΓΗΣ ΤΩΝ ΚΟΥΝΕΛΙΩΝ

Ο Leonardo Pisano Fibonacci (1170-1240) γεννήθηκε στην Πίζα. Ο πατέρας του Leonardo, Guilielmo Bonacci, ήταν γραμματέας της Δημοκρατίας της Πίζας στη Βορειοαφρικανική πόλη Bugia. Ο Fibonacci μεγάλωσε εκεί και η εκπαίδευσή του επηρεάστηκε σημαντικά από τους Μαυριτανούς αλλά και από τα ταξίδια που έκανε αργότερα κατά μήκος της Μεσογειακής ακτής (Αίγυπτο, Συρία, Ελλάδα, Σικελία και Προβηγκία). Έτσι, μελέτησε και έμαθε τις μαθηματικές τεχνικές και τα αριθμητικά συστήματα που είχαν υιοθετηθεί σε εκείνες τις περιοχές.

Γύρω στο 1200, ο Fibonacci επέστρεψε στην Πίζα, όπου για τα επόμενα 25 χρόνια επεξεργαζόταν τις δικές του μαθηματικές συνθέσεις. Στο βιβλίο του με τίτλο "Liber Abaci",  εισήγαγε την έννοια της ακολουθίας στα Μαθηματικά της Δυτικής Ευρώπης. Σ’ έναν περίφημο, πλέον, συλλογισμό, προσπάθησε να υπολογίσει την ταχύτητα αναπαραγωγής των κουνελιών στη γη, κάτω από ιδανικές συνθήκες. Ο Fibonacci υπέθεσε ότι έχουμε 1 ζευγάρι κουνελιών, το οποίο αρχίζει να αναπαράγεται από τον πρώτο μήνα και μετά από κάθε μήνα κύησης, φέρνει στον κόσμο ένα ακόμη ζευγάρι. Κάθε νέο ζευγάρι είναι έτοιμο να τεκνοποιήσει 1 μήνα μετά τη γέννησή του, γεννά 1 μήνα μετά και συνεχίζει να αναπαράγεται με τον ίδιο ρυθμό. Πόσα ζευγάρια κουνελιών θα έχουμε στο τέλος του πρώτου χρόνου;

1. Αρχικά υπάρχει ένα ζευγάρι κουνελιών.
2. Στο τέλος του 1ου μήνα το αρχικό ζευγάρι είναι έτοιμο να ζευγαρώσει, αλλά υπάρχει μόνο αυτό.
3. Στο τέλος του 2ου μήνα έχουμε το αρχικό ζευγάρι και το πρώτο ζευγάρι παιδιών του. Συνολικά 2 ζευγάρια κουνελιών. 
4. Στο τέλος του 3ου μήνα έχουμε το αρχικό ζευγάρι, το πρώτο ζευγάρι παιδιών του, (που είναι έτοιμα κι αυτά να τεκνοποιήσουν) και ένα δεύτερο ζευγάρι παιδιών του. Συνολικά 3 ζευγάρια κουνελιών. 
5. Στο τέλος του 4ου μήνα έχουμε το αρχικό ζευγάρι, το πρώτο ζευγάρι παιδιών και το πρώτο δικό του ζευγάρι παιδιών, το δεύτερο ζευγάρι παιδιών, που είναι έτοιμα να τεκνοποιήσουν, και ένα νέο, τρίτο ζευγάρι παιδιών. Συνολικά 5 ζευγάρια κουνελιών. 

Με βάση αυτή την υπόθεση, ο Fibonacci ανακάλυψε ότι τα ζευγάρια των κουνελιών αυξάνονταν κάθε μήνα σύμφωνα με μια άπειρη ακολουθία αριθμών: 
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 114, 233, 377, 610...

Μπορείτε να εντοπίσετε το μοτίβο που κρύβεται πίσω από αυτή την αλληλουχία; 

Οι αριθμοί αυτοί ονομάστηκαν «αριθμοί Fibonacci» και αποτελούν τη λεγόμενη «Ακολουθία Fibonacci». Εκτός από τους δύο πρώτους αριθμούς που είναι το 1, κάθε αριθμός της ακολουθίας Fibonacci ισούται με το άθροισμα των δύο προηγουμένων: 

α_ν+2 = α_ν+1 + α_ν

Αν και υπάρχουν αναφορές ότι αυτή η ακολουθία είχε αναφερθεί περίπου μισό αιώνα πριν, από τους Ινδούς Gospala και Hemachandra, ο Fibonacci συνάντησε αυτή την ακολουθία μελετώντας την Μεγάλη Πυραμίδα του Χέοπα στην Αίγυπτο, η οποία και είναι χτισμένη με βάση τον αριθμό  φ.

Όμως, τι σχέση έχει η ακολουθία Fibonacci με το χρυσό αριθμό; 

Κατασκευάζουμε μια ακολουθία με τους λόγους των διαδοχικών όρων της ακολουθίας Fibonacci.

Μπορούμε να πάρουμε ένα κομπιουτεράκι και να κάνουμε τις διαιρέσεις. Θα διαπιστώσουμε πως όσο προχωράμε στην ακολουθία, το πηλίκο θα προσεγγίζει όλο και περισσότερο τον αριθμό φ.

π.χ.
5/3=1,66666666...
89/55=1,6181818...
377/233=1,618025751
987/610=1,618032787
46368/28657=1,618033988

Σε μαθηματικούς όρους, αυτό σημαίνει πως η ακολουθία των λόγων δύο διαδοχικών αριθμών Fibonacci έχει ως όριο τον αριθμό φ. Το συμπέρασμα αυτό αποδείχτηκε από τον μαθηματικό Robert Simpson το 1753, δηλαδή πεντέμιση αιώνες αργότερα από τον ορισμό της ακολουθίας από τον Fibonacci!

Εμβαθύνοντας λίγο στην Ανάλυση...

Όπως κάθε ακολουθία που προσδιορίζεται από αναδρομική σχέση, έτσι και η ακολουθία Fibonacci έχει έναν τύπο κλειστής μορφής, δηλαδή έναν γενικό τύπο που δίνει τον ν-οστό όρο. Αυτός είναι γνωστός ως τύπος του Binet:

Υπολογίζεται το όριο της ακολουθίας των λόγων δύο διαδοχικών όρων της F(n):

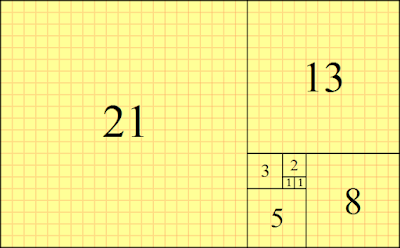
Παρόμοια, οι αριθμοί Fibonacci προσεγγίζουν εντυπωσιακά και τη χρυσή έλικα. Παρακάτω βλέπουμε μια κάλυψη του επιπέδου με τετράγωνα, οι πλευρές των οποίων είναι διαδοχικοί αριθμοί Fibonacci.

Ενώνουμε κάθε φορά δύο απέναντι κορυφές των τετραγώνων γράφοντας τόξα κύκλων. Σχηματίζεται η έλικα (ή σπείρα) Fibonacci, η οποία αποτελεί προσέγγιση της χρυσής έλικας. 

Η χρυσή αναλογία συνδέεται, δηλαδή, με τον πολλαπλασιασμό των κουνελιών, παρόλο που η Ακολουθία Fibonacci σχηματίστηκε ανεξάρτητα από την ευκλείδεια γεωμετρία. 

Ο φ ΚΑΙ Η ΑΛΓΕΒΡΑ

• Υπολογισμός του φ:

Για να υπολογίσουμε την τιμή του φ, ξεκινάμε από τον ορισμό:

Απλοποιώντας το αριστερό κλάσμα και αντικαθιστώντας το b/a = 1/φ, παίρνουμε

άρα,

Πολλαπλασιάζοντας και τα δύο μέλη με φ, παίρνουμε: φ + 1 = φ²

επομένως προκύπτει η εξίσωση: φ² – φ – 1 = 0

Χρησιμοποιώντας τη μέθοδο επίλυσης εξισώσεων 2^ου βαθμού, με διακρίνουσα, βρίσκουμε:

Επειδή το φ εκφράζει αναλογία μεταξύ θετικών ποσοτήτων, το φ είναι αναγκαστικά θετικό:

• Ιδιότητες:

1) Αν ελαττώσουμε τον φ κατά 1 μονάδα, αντιστρέφεται!

Επειδή φ = 1 + 1/φ , προκύπτει ότι 

2) Αν υψώσουμε τον φ στο τετράγωνο, αυξάνεται κατά 1 μονάδα!

Επειδή φ² = 1 + φ, παίρνουμε 

και αυτό μπορεί να συνεχιστεί επ’ άπειρον.

3) Ακόμα, για τον αριθμό φ ισχύει ότι:

• φ = 1φ
• φ² = 1φ + 1
• φ³ = 2φ + 1
• φ⁴ = 3φ + 2
• φ⁵ = 5φ + 3
• φ⁶ = 8φ + 5 …

Παρατηρούμε, δηλαδή, ότι στις δυνάμεις του φ «κρύβεται» η ακολουθία Fibonacci!

Η παραπάνω έκφραση μπορεί να χρησιμοποιηθεί για την ανάλυση μεγάλων δυνάμεων φⁿ σε έναν γραμμικό συνδυασμό του φ και του 1. Η σχέση που προκύπτει παράγει αριθμούς Fibonacci ως γραμμικούς συντελεστές:

φⁿ =  F(n) φ + F(n-1)

4) Μια άλλη έκφραση του αριθμού φ βασισμένη μόνο στο ψηφίο του 5 είναι η παρακάτω και οφείλεται στον Erol Karazincir:

ΠΑΝΤΑΧΟΥ ΠΑΡΩΝ…

Το Σύμπαν δείχνει να τρέφει μια ιδιαίτερη αδυναμία για τον αριθμό φ με τα άπειρα δεκαδικά ψηφία. 

(Συνεχίζεται...)

Πηγές:

Περιοδικό Focus

goldennumber.net

wikipedia.org
Πανεπιστημιακές σημειώσεις "Ευκλείδεια και μη Ευκλείδειες Γεωμετρίες" καθηγητή Χρ.Μπαϊκούση, 2011

Μετρώντας τη Γη: Ο μεγαλοφυής υπολογισμός του Ερατοσθένη

Η πρώτη φορά στην ιστορία κατά την οποία έγινε πραγματική μέτρηση για τον υπολογισμό της περιμέτρου της Γης, ήταν από τον Ερατοσθένη τον Κυρηναίο (276 πΧ – 194 πΧ), ο οποίος υπολόγισε με εκπληκτική ακρίβεια την περίμετρο της Γης από... ένα πηγάδι. Για τη μέτρηση αυτή ο Ερατοσθένης είχε γράψει ιδιαίτερη πραγματεία, όπως πληροφορούμαστε από την «Διόπτρα» του Ήρωνος του Αλεξανδρέως, ο οποίος αναφερόμενος στο μέγεθος της περιμέτρου της Γης σημειώνει: «Ερατοσθένης εν τω επιγραφομένω περί αναμετρήσεως της Γης».

Ο Ερατοσθένης γεννήθηκε στην ελληνική αποικία της Βόρειας Αφρικής, Κυρήνη και ήταν φίλος με τον Αρχιμήδη. Λέγεται ότι είχε ζήσει στην Αθήνα για αρκετά χρόνια, ώσπου έγινε βιβλιοθηκάριος στην περίφημη βιβλιοθήκη της Αλεξάνδρειας, όπου και μελετούσε.

Πώς ένα πηγάδι βοήθησε τον Ερατοσθένη να αποδείξει ότι η Γη είναι στρογγυλή...

Η άποψη ότι η Γη ήταν σφαιρική ήταν αποδεκτή στην αρχαία Ελλάδα. Ο Ερατοσθένης ήταν εκείνος που απέδειξε μαθηματικά αυτή την πεποίθηση και μάλιστα υπολόγισε με αξιοθαύμαστη ακρίβεια την ακτίνα και την περίμετρο της σφαιρικής Γης.

Την εποχή που βρισκόταν στη βιβλιοθήκη, ο Ερατοσθένης πληροφορήθηκε για ένα πολύ περίεργο πηγάδι, το οποίο βρισκόταν κοντά στη Συήνη (σημερινό Ασουάν της νότιας Αιγύπτου). Κάθε χρόνο, το μεσημέρι της 21ης Ιουνίου - τη μέρα του θερινού ηλιοστασίου, δηλαδή τη μεγαλύτερη μέρα του έτους - ο Ήλιος καθρεφτιζόταν ολόκληρος μέσα στο πηγάδι και το φώτιζε μέχρι τον πυθμένα του, χωρίς να δημιουργείται σκιά γύρω από αυτό. Ο Ερατοσθένης συμπέρανε ότι για να συμβαίνει κάτι τέτοιο, τη συγκεκριμένη μέρα ο Ήλιος έπρεπε να βρίσκεται ακριβώς κατακόρυφα πάνω από το πηγάδι.

Ο ήλιος όμως δεν συμπεριφερόταν το ίδιο και στα βόρεια της Αιγύπτου. Στην Αλεξάνδρεια, η οποία απέχει 800 χλμ από το Ασουάν, την ίδια εκείνη μέρα, ο ήλιος δημιουργούσε μια μικρή σκιά σε μια ψηλή κολώνα. Αυτό σήμαινε ότι οι δύο πόλεις σίγουρα δεν έβλεπαν τον ήλιο υπό την ίδια γωνία. Ο Ερατοσθένης γνώριζε ήδη από προγενέστερες αστρολογικές μετρήσεις που διάβασε στη βιβλιοθήκη ή από δικούς του υπολογισμούς, ότι η Συήνη και η Αλεξάνδρεια ανήκαν στον ίδιο μεσημβρινό. Επομένως ο λόγος που ο Ήλιος δεν μπορούσε να μεσουρανεί ταυτόχρονα στη Συήνη και στην Αλεξάνδρεια οφειλόταν στο ότι η Γη ήταν στρογγυλή και όχι επίπεδη. 

Πώς ο Ερατοσθένης υπολόγισε την περίμετρο της Γης...

Το πείραμα του Ερατοσθένη βασίστηκε στη μέτρηση της γωνίας υπό την οποία ο Ήλιος έστελνε τις ακτίνες του σε δύο διαφορετικές τοποθεσίες (Αλεξάνδρεια και Συήνη), την ίδια χρονική στιγμή.  Ο Ερατοσθένης πραγματοποίησε το πείραμα στις 21 Ιουνίου, την ημέρα του θερινού ηλιοστασίου, όταν η Γη παρουσιάζει τη μέγιστη κλίση της ως προς τον Ήλιο. Αυτό σημαίνει ότι ο Ήλιος το μεσημέρι βρισκόταν ακριβώς πάνω από τις δύο πόλεις.

Στο σχήμα βλέπουμε παράλληλες ακτίνες να φτάνουν από τον Ήλιο στη Γη. Το μεσημέρι της 21^ης Ιουνίου, οι ηλιακές ακτίνες βυθίζονται στο πηγάδι της Συήνης, χωρίς να δημιουργούν καμία σκιά, επομένως «κατευθύνονται» προς το κέντρο της Γης. 

Την ίδια χρονική στιγμή στην Αλεξάνδρεια, μία ψηλή κολώνα (κάθετη στο έδαφος) σχηματίζει μια μικρή σκιά. Ο Ερατοσθένης μέτρησε το ύψος της κολώνας και το μήκος της σκιάς της. Έτσι δημιούργησε ένα ορθογώνιο τρίγωνο και, χρησιμοποιώντας την τριγωνομετρία, υπολόγισε τη γωνία που σχηματιζόταν ανάμεσα στην κολώνα και στις ακτίνες του Ήλιου. Το αποτέλεσμα ήταν ότι η γωνία ήταν φ = 7,2˚ , δηλαδή το 1/50 της περιφέρειας του κύκλου που είναι 360˚.

Εδώ έχει μεγάλη σημασία το ότι η γωνία φ ισούται με τη γωνία που σχηματίζεται ανάμεσα στις δύο ακτίνες που συνδέουν το κέντρο της Γης με την Αλεξάνδρεια και τη Συήνη αντίστοιχα (εντός εναλλάξ γωνίες).

Στη συνέχεια, με την βοήθεια του βασιλιά Πτολεμαίου, ο οποίος διέθεσε ένα είδος οδομέτρου με γρανάζια, μέτρησε την απόσταση των δύο πόλεων, που ήταν 5.040 στάδια. Στο πείραμα του, τα 5.040 στάδια αντιστοιχούσαν στο 1/50 της περιφέρειας του κύκλου.

Τέλος, πολλαπλασίασε το 5.040 με το 100% του κύκλου, δηλαδή το 50, και έτσι υπολόγισε την περίμετρο της Γης στα 252.000 στάδια, ή με τη σύγχρονη μονάδα μέτρησης, 39.690 χιλιόμετρα. Ο υπολογισμός που έκανε ο Ερατοσθένης 2.200 χρόνια πριν ήταν αρκετά ακριβής. Σήμερα η περίμετρος της Γης υπολογίζεται σύμφωνα με δορυφορικές μετρήσεις σε 40.048 χιλιόμετρα, άρα στην ουσία έπεσε έξω μόλις 358 χιλιόμετρα!

Πηγες:

Τζόνι Μπολ, Μαθημαγικά, Εκδόσεις Polaris, 2011

wikipedia.org