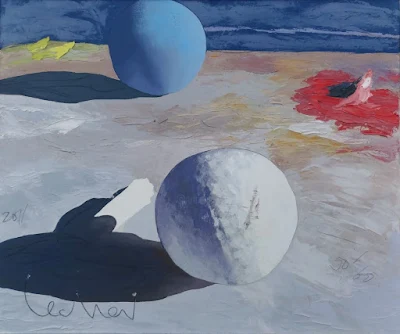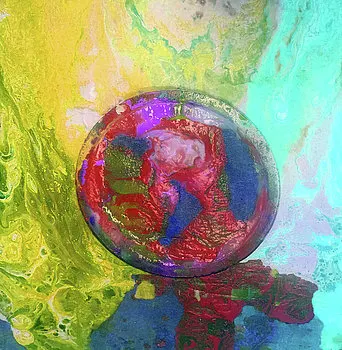Εμφάνιση αναρτήσεων με ετικέτα στερεά εκ περιστροφής. Εμφάνιση όλων των αναρτήσεων
Εμφάνιση αναρτήσεων με ετικέτα στερεά εκ περιστροφής. Εμφάνιση όλων των αναρτήσεων

Σάββατο 2 Μαΐου 2020

Τα Μαθηματικά στην Τέχνη: Τόρος και τοροειδή πολύεδρα


ΤΟΡΟΣ

Τα βιβλία γράφουν...

Τόρος είναι η επιφάνεια που παράγεται από την περιστροφή ενός κύκλου γύρω από έναν άξονα συνεπίπεδο με τον κύκλο.

Αντίστοιχα, στερεός τόρος είναι το στερεό που παράγεται από την περιστροφή ενός κυκλικού δίσκου γύρω από έναν άξονα συνεπίπεδο με τον κυκλικό δίσκο.

π.χ. Ένα φουσκωτό σωσίβιο είναι τόρος, ενώ ένα ντόνατ είναι στερεός τόρος.

Δεν ήταν λίγοι οι καλλιτέχνες που εμπνεύστηκαν και από τον τόρο...



Σελίδα από το βιβλίο του Johannes Lencker "Perspectiva Literaria" ("Λογοτεχνική Προοπτική", Νυρεμβέργη, 1567) 

Wayne Ferrebee (Σύγχρονος ζωγράφος) - "Donut Universe with Centaur and Mummy" (2010)

Wayne Ferrebee (Σύγχρονος ζωγράφος) - "Torus with Spearman, Bagpipes and Barnacle" (2011)

Seth Bareiss (γεν. 1964) - "Torus, Fish, Hawks and Horses" (2007)

Don Barrett (Σύγχρονος γραφίστας) - "Torus"

Marta Banaszak (γεν. 1975) - "Kamasutra Torus Black" (2014)

Marta Banaszak (γεν. 1975) -
"Kamasutra Torus Black" (2014)

Amer Kobaslija (Σύγχρονος καλλιτέχνης) - "Lowe's Tubes, Ichetucknee" (2018)

Terry Romero Paul (Σύγχρονη ζωγράφος) - "Penny Lane"

DAN (Κοσμολόγος και ζωγράφος, γεν. 1968) - "Double Torus Universe" (2010)
Σύμφωνα με πολλούς μελετητές, το σύμπαν μας έχει σχήμα τόρου. Δεν έχει λοιπόν αρχή και τέλος, υπακούοντας στην Αρχή Διατήρησης της Ενέργειας.


Ο τόρος εισάγει μια νέα κατηγορία επιφανειών, αυτών που έχουν "τρύπα". Το πλήθος των τρυπών της επιφάνειας ονομάζεται γένος της επιφάνειας. Από τοπολογική άποψη, οι επιφάνειες του ίδιου γένους θεωρούνται ομοιομορφικοί, δηλαδή "ίδιοι".




ΤΟΡΟΕΙΔΗ ΠΟΛΥΕΔΡΑ

 Τα βιβλία γράφουν...

Τα πολύεδρα με τοπολογικό τύπο τόρου λέγονται τοροειδή πολύεδρα και έχουν χαρακτηριστική Euler χ = Κ - Α + Ε = 0.

Leonardo da Vinci (1452 - 1519) - Σχέδιο του Mazzocchio (αρχές 
16ου αιώνα)
Paolo Uccello (1397 - 1475) - Σχέδιο του Mazzocchio (μέσα
15ου αιώνα)
Paolo Uccello (1397 - 1475) -  Σχέδιο του Mazzocchio (μέσα
15ου αιώνα)

 Εκτός από τα πλατωνικά στερεά, ένα άλλο αγαπημένο γεωμετρικό στερεό των Αναγεννησιακών ζωγράφων ήταν ένα τοροειδές πολύεδρο, το οποίο αποκαλούσαν Μαζζόκιο (Mazzocchio). Το συγκεκριμένο στερεό αντιπροσώπευε το υψηλότερο επίπεδο δεξιοτεχνίας στην εξάσκηση της προοπτικής για γεωμετρικά στερεά.
Wentzel Jamnitzer (1508 - 1585) - Σχέδιο του Mazzocchio (μέσα
16ου αιώνα)


Peter Halt - Σχέδιο του Mazzocchio (αρχές 17ου αιώνα)

Αναγεννησιακό ξυλόγλυπτο (Intarsia), έργο του Fra Giovanni da Verona (1457 - 1525). Μοναστήρι του Monte Olivetto, κοντά στη Siena (περ. 1503 - 1506). Απεικονίζει μια 72-εδρη σφαίρα (σφαίρα του Κάμπανου) και ένα τοροειδές πολύεδρο (Mazzocchio)
Mimmo Paladino (γεν. 1948) - Γλυπτό στο Μουσείο Βωμός της Ειρήνης, Ρώμη
Πηγές:
Αναρτήθηκε από στις 7 σχόλια:
Ετικέτες , , , , ,

Κυριακή 5 Απριλίου 2020

Τα Μαθηματικά στην Τέχνη: Σφαίρα και σφαιρικά πολύεδρα


ΣΦΑΙΡΑ

 Τα βιβλία γράφουν...

Σφαίρα είναι το σχήμα που παράγεται από την περιστροφή ενός κύκλου (Ο, ρ) με άξονα περιστροφής μια διάμετρό του.


Τα βιβλία επίσης γράφουν...

Σφαίρα είναι το σύνολο των σημείων Μ του χώρου που απέχουν από ένα σταθερό σημείο Ο σταθερή απόσταση ρ, δηλαδή ισχύει:
ΟΜ = ρ.

Rene Magritte (1898 - 1967)

Rene Magritte (1898 - 1967) - "L'ombre Monumentale" (1932)

Ivan Kliun (1873- 1943) - "Σφαιρική μη αντικειμενική σύνθεση" (1922-25)

A.J. Edwards (Σύγχρονος καλλιτέχνης) - "Game Room"

Barbara Fox (Σύγχρονη ζωγράφος) - "Billiard Balls - Still Life"

Georgi Lechev (Σύγχρονος καλλιτέχνης) - "Dialog Between White and Blue" (2011)

Allen Donnelly (Σύγχρονος καλλιτέχνης και συγγραφέας) - "On the beach"

James Pikerton (σύγχρονος ζωγράφος) - "Shadow Spheres" (2015)

James Pikerton (σύγχρονος ζωγράφος) - "Sphere Orb"

James Pikerton (σύγχρονος ζωγράφος) - "Red Sphere"

Katie Morris (Σύγχρονη ζωγράφος και καθηγήτρια καλλιτεχνικών) - "Sports Spheres"
Μέσα από τις καλλιτεχνικές δραστηριότητες στη σχολική τάξη, προσπαθεί να διδάξει στους μαθητές της τα γεωμετρικά σχήματα και τα γεωμετρικά στερεά. 

Katie Morris (Σύγχρονη ζωγράφος και καθηγήτρια καλλιτεχνικών) - "Sports Spheres"

Katie Morris (Σύγχρονη ζωγράφος και καθηγήτρια καλλιτεχνικών) - "Sports Spheres"

Katie Morris (Σύγχρονη ζωγράφος και καθηγήτρια καλλιτεχνικών) - "Sports Spheres"

Katie Morris (Σύγχρονη ζωγράφος και καθηγήτρια καλλιτεχνικών) - "Sports Spheres"

Katie Morris (Σύγχρονη ζωγράφος και καθηγήτρια καλλιτεχνικών) - "Sports Spheres"

Russell Kightley (Σύγχρονος καλλιτέχνης) - "Sphere Equations"



Τι γίνεται όταν επιτρέψουμε στα πολύεδρα να έχουν καμπυλωτές ακμές και έδρες;


ΣΦΑΙΡΙΚΑ ΠΟΛΥΕΔΡΑ

Τα βιβλία γράφουν...

 Η επιφάνεια της σφαίρας μπορεί να χωριστεί με ευθύγραμμα τμήματα σε οριοθετούμενες περιοχές, για να σχηματίσει ένα σφαιρικό πολύεδρο. Μεγάλο μέρος της θεωρίας των συμμετρικών πολυέδρων προκύπτει ευκολότερα με αυτόν τον τρόπο. Τα σφαιρικά πολύεδρα έχουν μια μακρά και αξιοσέβαστη ιστορία. Ο Poinsot, χρησιμοποιώντας σφαιρικά πολύεδρα, ανακάλυψε τα τέσσερα κανονικά αστεροειδή πολύεδρα. Τα πρώτα πολύεδρα που κατασκεύασε ο άνθρωπος ήταν σφαιρικά πολύεδρα σκαλισμένα σε πέτρα.
Paolo Uccello (1397 - 1475) - "Γεωμετρική Σφαίρα"
Martino da Udine (1470 - 1548) - Σπουδή στη Γεωμετρία και στην προοπτική

.*.〰.*.〰.*.〰.*.〰.*.〰.*.〰.*.

"Μεταχειρίσου τη φύση μέσω του κυλίνδρου, της σφαίρας και του κώνου, όλα τοποθετημένα με προοπτική, ώστε κάθε πλευρά ενός αντικειμένου ή ενός επιπέδου να κατευθύνεται προς ένα κεντρικό σημείο. Αν μάθουμε να βασίζουμε τη ζωγραφική μας πάνω σ' αυτά τα απλά σχήματα, θα μπορέσουμε να πετύχουμε τα πάντα".
Paul Cezanne (1839 - 1906)

.*.〰.*.〰.*.〰.*.〰.*.〰.*.〰.*.


Πηγές:
Αναρτήθηκε από στις 3 σχόλια:
Ετικέτες , , , ,

Κυριακή 1 Μαρτίου 2020

Τα Μαθηματικά στην Τέχνη: Κώνος


ΚΩΝΟΣ
Τα βιβλία γράφουν...

Ορθός κώνος ή κώνος εκ περιστροφής ή απλώς κώνος λέγεται το στερεό σχήμα που παράγεται από την περιστροφή ενός ορθογωνίου τριγώνου γύρω από μία κάθετη πλευρά του.

Christofer Andrukiewicz (Σύγχρονος ζωγράφος) - "Lady in a Cone Hat"

Terry Romero Paul (Σύγχρονη ζωγράφος) - "Melted Coffee Ice Cream" (2018)

Terry Romero Paul (Σύγχρονη ζωγράφος) - "Cones and More Cones" (2014)

Wayne Thiebaud (γεν. 1920) - "Clown Cones" (2000)

Gerhard Richter (Σύγχρονος ζωγράφος) - "Kegel (Cone)" (1985)

Russell Kightley (Σύγχρονος καλλιτέχνης) - "Cone"


ΚΟΛΟΥΡΟΣ ΚΩΝΟΣ


Τα βιβλία γράφουν...

Κόλουρος κώνος λέγεται το στερεό σχήμα που παράγεται από την περιστροφή ενός ορθογωνίου τραπεζίου γύρω από την κάθετη προς τις βάσεις πλευρά του.

Scott Budgell (a.k.a. Jazzberry Blue) (Σύγχρονος graphic artist) - "Conical Frustum"


ΚΩΝΙΚΕΣ ΤΟΜΕΣ
Τα βιβλία γράφουν...

 Κωνική τομή ονομάζεται μια καμπύλη που προκύπτει από την τομή κώνου και επιπέδου, ή ακριβέστερα, από την τομή ενός επιπέδου με δύο ίσες ορθές άπειρες κωνικές επιφάνειες που έχουν κοινό άξονα και συνδέονται στην κορυφή τους. Η θέση του επιπέδου ως προς τον κώνο καθορίζει τη μορφή της κωνικής τομής:

  • Αν το επίπεδο είναι κάθετο στον άξονα του κώνου, η κωνική τομή είναι ένας κύκλος.
  • Αν το επίπεδο δεν είναι κάθετο στον άξονα του κώνου και τέμνει όλες τις γενέτειρες αυτού, η κλειστή καμπύλη που δημιουργείται είναι μια έλλειψη.
  • Αν το επίπεδο είναι παράλληλο προς μια γενέτειρα του κώνου, η κωνική τομή είναι παραβολή.
  • Αν το επίπεδο δεν είναι κάθετο στον άξονα του κώνου και ούτε παράλληλο προς μια γενέτειρα αυτού, τότε η κωνική τομή είναι υπερβολή.
  • Τέλος, αν το επίπεδο διέρχεται από την κορυφή του κώνου, η τομή λέγεται εκφυλισμένη κωνική τομή και στην περίπτωση αυτή έχουμε ένα σημείο ή ένα ζεύγος ευθειών που διέρχονται από την κορυφή του κώνου.
Russell Kightley (Σύγχρονος καλλιτέχνης) - "Conic Sections"
Πηγές:
Αναρτήθηκε από στις 5 σχόλια:
Ετικέτες , , , ,

Σάββατο 1 Φεβρουαρίου 2020

Τα Μαθηματικά στην Τέχνη: Στερεά εκ περιστροφής - Κύλινδρος


Στο πλαίσιο του πρότζεκτ "Τα Μαθηματικά στην Τέχνη" γνωρίσαμε μέσω της τέχνης την πρώτη οικογένεια γεωμετρικών στερεών, που ήταν τα πολύεδρα. Συγκεκριμένα, είδαμε τον κύβο, το ορθογώνιο παραλληλεπίπεδο, τις πυραμίδες, τα πρίσματα, τα πλατωνικά στερεά, τα αρχιμήδεια στερεά, διάφορα επιπλέον κυρτά πολύεδρα και τέλος διάφορα μη κυρτά και αστεροειδή πολύεδρα. Τα στερεά εκ περιστροφής είναι η δεύτερη οικογένεια στερεών που θα μάθουμε μέσα από το πρότζεκτ αυτό. 


ΣΤΕΡΕΑ ΚΑΙ ΕΠΙΦΑΝΕΙΕΣ ΕΚ ΠΕΡΙΣΤΡΟΦΗΣ


 Τα βιβλία γράφουν...

Τα στερεά εκ περιστροφής δημιουργούνται κατά την περιστροφή ενός επίπεδου σχήματος γύρω από άξονα περιστροφής (μια ευθεία) ο οποίος βρίσκεται στο ίδιο επίπεδο με το αρχικό επίπεδο σχήμα.

Όμοια, οι επιφάνειες εκ περιστροφής δημιουργούνται κατά την περιστροφή μιας επίπεδης γραμμής γύρω από άξονα περιστροφής που βρίσκεται στο επίπεδο της γραμμής. Τα σημεία της γραμμής αυτής, που λέγεται γενέτειρα, κατά την περιστροφή γράφουν κύκλους που βρίσκονται σε επίπεδα κάθετα στον άξονα περιστροφής και έχουν τα κέντρα τους στον άξονα αυτό.
Δηλαδή όταν μιλάμε για επιφάνεια εκ περιστροφής, εννοούμε την εξωτερική επιφάνεια του στερεού.

Δείτε εδώ ένα παράδειγμα δημιουργίας στερεού εκ περιστροφής στο Geogebra.

Στα επόμενα θα γνωρίσουμε τα σημαντικότερα στερεά εκ περιστροφής.


ΚΥΛΙΝΔΡΟΣ

Andy Warhol (1928 - 1987) - "Cambell's Soup Can" (Μέρος της σειράς "Cambell's Soup Cans" από 32 πίνακες του 1962)

Terrie Lombardi (Σύγχρονη ζωγράφος) - "Mashine Shop in Taos"

Wayne Thiebaud (γεν. 1920) - "Candies" (1966)

Wayne Thiebaud (γεν. 1920)

Wayne Thiebaud (γεν. 1920) - "Two Paint Cans" (1987)

Robbie Allen (Σύγχρονος ζωγράφος) - "Burning the Midnight Oil" (2017)

Serhiy Naberezhnykh (γεν. 1956) - "Cylinders"

Russell Kightley (Σύγχρονος καλλιτέχνης) - "Cylinder Equations"

Russell Kightley (Σύγχρονος καλλιτέχνης) - "Cylinder Equations"

Scott Budgell (a.k.a. Jazzberry Blue) (Σύγχρονος graphic artist) - "Cylinder"


Τα βιβλία γράφουν...

Ορθός κυκλικός κύλινδρος ή κύλινδρος εκ περιστροφής ή απλώς κύλινδρος λέγεται το σχήμα που παράγεται από ένα ορθογώνιο παραλληλόγραμμο, το οποίο εκτελεί μία πλήρη περιστροφή στο χώρο γύρω από τη μία πλευρά του.


Πηγές:
Αναρτήθηκε από στις 3 σχόλια:
Ετικέτες , ,
Εγγραφή σε: Αναρτήσεις (Atom)