Περί του χρυσού αριθμού «φ»... (Μέρος 2º - Ο αριθμός «φ», πανταχού παρών!)

«Όλη η ζωή είναι βιολογία

Όλη η βιολογία είναι φυσιολογία

Όλη η φυσιολογία είναι χημεία

Όλη η χημεία είναι φυσική

Όλη η φυσική είναι μαθηματικά».

Dr. Stephen Marquardt

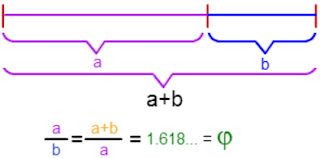
Μελέτες σε πολλούς κλάδους όπως η Βιολογία, η Βοτανολογία και η  Ζωολογία δείχνουν πως ο σχεδιασμός της ζωής βασίζεται σε έναν «χρυσό κανόνα»… Σχεδόν παντού μπορεί να εντοπιστεί ο χρυσός αριθμός φ και η ακολουθία Fibonacci που διαβάσατε εδώ … Υπενθυμίζουμε ότι αριθμός φ ισούται περίπου με 1,61803398874989484... και η ακολουθία Fibonacci είναι η εξής: 

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 114, 233, 377, 610...

Ο ΑΡΙΘΜΟΣ φ ΣΤΗ ΦΥΣΗ ΚΑΙ ΣΤΑ ΦΥΤΑ

Τα φυτά «κρύβουν» την ακολουθία Fibonacci στον αριθμό ή στη διάταξη των φύλλων, των πετάλων, των κλαδιών ή των σπόρων. Φυσικά και δε γνωρίζουν για την ακολουθία Fibonacci - απλά μεγαλώνουν με τον πιο αποτελεσματικό τρόπο.

Για παράδειγμα, στην κυκλική διάταξη της στεφάνης του τριαντάφυλλου, τα πέταλα διατάσσονται όπως τα σκαλοπάτια μιας ελικοειδούς σκάλας. Η γωνία ανάμεσα σε 2 πέταλα είναι περίπου 222,5 μοίρες. Αν διαιρέσουμε τις 360 μοίρες του κύκλου με τον αριθμό 222,5, το πηλίκο είναι, κατά μεγάλη προσέγγιση, ο αριθμός φ = 1,618... Αυτό δεν είναι τυχαίο... Σύμφωνα με μετρήσεις, σ’ αυτήν ακριβώς τη γωνία των 222,5 μοιρών, τα φύλλα των φυτών ρίχνουν την ελάχιστη δυνατή σκιά το ένα στο άλλο.

Επιπλέον, σε κάθε σειρά πετάλων, υπάρχουν συνήθως είτε 5, είτε 8, είτε 13 πέταλα.

Στη φωτογραφία παρακάτω βλέπουμε μια μικρή μαργαρίτα. Στο κέντρο του λουλουδιού σχηματίζονται σπείρες, σύμφωνα με τη ακολουθία Fibonacci.

Υπάρχουν 21 σκούρες μπλε σπείρες και 13 γαλάζιες σπείρες. Το 13 και το 21 είναι διαδοχικοί αριθμοί στην ακολουθία Fibonacci. Παρόμοιες διατάξεις εμφανίζουν πολλά ακόμη άνθη...

Οι σπόροι του ηλίανθου κατανέμονται κυκλικά. Η σπείρα είναι προς τα έξω ενώ έχει διπλή κατεύθυνση, δηλαδή και όπως κινούνται οι δείκτες του ρολογιού και αντίστροφα από το κέντρο του λουλουδιού.  

Ο αριθμός των σπειρών στο κάθε φυτό δεν είναι ίδιος. Γιατί  γενικά είναι είτε 21 και 34, είτε 34 και 55, είτε 55 και 89, ή 89 και 144; Ο αριθμός των σπειρών ενός ηλίανθου και προς τις δύο κατευθύνσεις είναι δύο διαδοχικοί αριθμοί στην ακολουθία Fibonacci. 

Αν μετρήσει κανείς τα πέταλα ενός λουλουδιού, θα διαπιστώσει ότι ο αριθμός τους είναι συχνά 3, 5, 8, 13, 21, 34 ή ακόμα και 55 ή 89. 

Για παράδειγμα, μπορούμε να μετρήσουμε στις μαργαρίτες 13, 21, 34, 55, ή και 89 πέταλα. Οι κοινές μαργαρίτες του αγρού έχουν συνήθως 34 πέταλα. Ο κρίνος έχει 3 πέταλα,  η νεραγκούλα έχει 5  κ.λπ. 

Έχει παρατηρηθεί ότι η ακολουθία Fibonacci εμφανίζεται στη φυλλοταξία πολλών φυτών.

Η ακολουθία Fibonacci εμφανίζεται και στις βελόνες αρκετών ειδών έλατου, στα φύλλα της λεύκας, της κερασιάς, της μηλιάς, της δαμασκηνιάς, της βελανιδιάς και της φιλύρας. Τη βλέπουμε στην επιφάνεια των κορμών των κωνοφόρων δέντρων, στους δακτύλιους των κορμών των φοινικόδεντρων και των κουκουναριών.

Όλα τα κουκουνάρια αναπτύσσονται σε σπείρες, ξεκινώντας από τη βάση όπου ήταν ο μίσχος, και πηγαίνοντας κυκλικά μέχρι να φτάσουμε στην κορυφή.

Συναντάμε την έλικα Fibonacci στο σχήμα της αλόης της πολύφυλλου, της αγκινάρας, του κουνουπιδιού,  του ανανά και πολλών άλλων φυτών, καρπών και λαχανικών.

Τέλος, παρατηρήστε τις αποστάσεις ανάμεσα στα κουκούτσια της μπανάνας και του μήλου. Μπορεί να περιμένατε συμμετρία στη φύση, αλλά αν κόψετε στη μέση ένα φρούτο ή λαχανικό, πιθανόν να ανακαλύψετε την ακολουθία Fibonacci…

Ο ΑΡΙΘΜΟΣ φ ΣΤΟ ΖΩΙΚΟ ΒΑΣΙΛΕΙΟ

Το κέλυφος των σαλιγκαριών ακολουθεί και αυτό την ακολουθία Fibonacci. Το ίδιο και το κέλυφος του ναυτίλου.

Η μόνη διαφορά μεταξύ των δύο είναι ότι το κέλυφος του ναυτίλου αναπτύσσεται σε τρισδιάστατες σπείρες, ενώ το κέλυφος των σαλιγκαριών αναπτύσσεται σε δισδιάστατες σπείρες.

ΠΑΡΘΕΝΟΓΕΝΕΣΗ ΣΤΟ ΜΕΛΙΣΣΙ

Μπορεί τα κουνέλια του Fibonacci να αποτελούν μια εξιδανικευμένη υπόθεση, αλλά μπορούμε να αναζητήσουμε κάποιο υπαρκτό παράδειγμα της ακολουθίας Fibonacci στη φύση. Και θα το βρούμε στο γενεαλογικό δέντρο κάθε κηφήνα σε ένα μελίσσι! Το εν λόγω έντομο, σε αντίθεση με τη βασίλισσα και τις εργάτριες, γεννιέται από ένα μη γονιμοποιημένο αβγό της βασίλισσας, δηλαδή έχει μητέρα αλλά όχι πατέρα. Επομένως το γενεαλογικό δέντρο του κηφήνα διαμορφώνεται ως εξής: Έχει 1 μητέρα, 2 παππούδες (αρσενικό και θηλυκό), 3 προπαππούδες (2 από την οικογένεια της γιαγιάς και 1 του παππού), 5 προ-προπαππούδες, 8 προ- προ-προπαππούδες κ.ο.κ. Το γενεαλογικό δέντρο του κηφήνα είναι μια ακολουθία Fibonacci!

Ο Leonardo de Pisa ή Fibonacci έζησε κοντά στην πόλη της Bejaia, η οποία αποτελούσε ένα σημαντικό εξαγωγέα κεριού την εποχή του Fibonacci (από εκεί προέρχεται και η γαλλική εκδοχή του ονόματος της πόλης αυτής, “bougie”, που σημαίνει" κερί "στα γαλλικά). Μια πρόσφατη μαθηματικο-ιστορική ανάλυση της περιόδου και της περιοχής στην οποία έζησε ο Fibonacci προτείνει ότι στην πραγματικότητα οι μελισσοκόμοι της Bejaia και οι γνώσεις τους σχετικά με την αναπαραγωγή των μελισσών αποτέλεσαν την πηγή έμπνευσης της ακολουθίας Fibonacci και όχι το ευρύτερα ίσως γνωστό μοντέλο της αναπαραγωγής κουνελιών.

Και όχι μόνο αυτό. Το 1966, ο Νταγκ Γιανέγκα από το Μουσείο Έρευνας στην εντομολογία του Πανεπιστημίου της Καλιφόρνια, ανακάλυψε ότι η αναλογία ανάμεσα σε εργάτριες μέλισσες και κηφήνες σε ένα μελίσσι προσεγγίζει πάντα τον αριθμό φ. 

Η παραπάνω πεταλούδα έχει στα φτερά της σημάδια που μοιάζουν με μάτια, τα οποία βρίσκονται στις χρυσές τομές των γραμμών που δείχνουν το μήκος και το πλάτος της. 

Ο κατάλογος στο ζωικό βασίλειο είναι ατελείωτος: το φ εμφανίζεται στα κέρατα του κριού, στο σώμα του δελφινιού, στον αστερία, στο σώμα και στα πόδια εντόμων όπως η αράχνη και το μυρμήγκι…

Ο ΑΡΙΘΜΟΣ φ ΣΤΟΝ ΜΙΚΡΟΚΟΣΜΟ

Ακόμα και πολλά από τα πιο μικρά σωματίδια στη φύση φαίνεται ότι διατάσσονται σύμφωνα με τη χρυσή αναλογία.

Πριν από λίγα χρόνια, Ελβετοί και Αμερικανοί επιστήμονες μελετούσαν τους λεγόμενους ημικρυστάλλους, οι οποίοι έχουν πολύ ιδιαίτερη δομή σε επίπεδο ατόμων. Η επιφάνειά τους αποτελείται από έδρες με δύο διαφορετικά ύψη. Όταν τα ύψη αυτά μετρήθηκαν μ’ ένα ακριβέστατο μικροσκόπιο σάρωσης σήραγγας (STM), οι ερευνητές έκπληκτοι ανακάλυψαν ότι ο λόγος του μεγαλύτερου ύψους προς το μικρότερο είναι φ = 1,618... 

Η θεωρία των ερευνητών είναι ότι ο κρύσταλλος έχει τη μεγαλύτερη σταθερότητα, όταν υπάρχει αυτή ακριβώς η σχέση. 

(Συνεχίζεται...)

Πηγές:

Περιοδικό Focus

goldennumber.net

wikipedia.org

1/6/2018: Παγκόσμια ημέρα του χρυσού αριθμού «φ»... (Μέρος 1º - Γνωριμία με τον αριθμό «φ»)

Τι κοινό έχουν οι ζωγραφικοί πίνακες της Αναγέννησης, το κουνουπίδι, η αναπαραγωγή των κουνελιών και μια πιστωτική κάρτα; Η απάντηση είναι ο αριθμός 1,61803398874989484..., ο "χρυσός αριθμός", ή "χρυσή αναλογία". Τα δεκαδικά του ψηφία είναι άπειρα και η ακολουθία τους δεν επαναλαμβάνεται. Μάθετε τι τον καθιστά τόσο μαγικό!

Όπως ο π (3,14) εκφράζει το πιο τέλειο γεωμετρικό σχήμα, τη σφαίρα, έτσι και ο φ (1,618) είναι ο αριθμός της «ομορφιάς». Ο μοναχός του 15^ου αιώνα Luca Pacioli, επηρεασμένος από την αντίληψη της εποχής ότι οι νέες γνώσεις της επιστήμης έπρεπε να ενταχθούν στο εκκλησιαστικό δόγμα, τον ονόμασε «Θεία Αναλογία» («Divina Proportione»). Ο Leonardo DaVinci τον ονόμασε «Χρυσό Αριθμό». Αιώνες αργότερα, ο μαθηματικός Mark Barr θα τον συμβόλιζε με το ελληνικό γράμμα φ, προς τιμήν του γλύπτη Φειδία, ο οποίος ήταν από τους πρώτους που δημιουργούσαν έργα με βάση τον αριθμό αυτό.

ΤΑ ΕΥΘΥΓΡΑΜΜΑ ΤΜΗΜΑΤΑ ΤΟΥ ΕΥΚΛΕΙΔΗ

Η αφετηρία είναι γεωμετρική. Ο Ευκλείδης στα «Στοιχεία» έδωσε τον πρώτο γραπτό ορισμό της χρυσής τομής, την οποία ονόμασε «άκρος και μέσος λόγος».

Ο Ευκλείδης παίρνει ένα ευθύγραμμο τμήμα και το διαιρεί σε δύο τμήματα. Η χρυσή τομή είναι εκείνο το σημείο που χωρίζει το ευθύγραμμο τμήμα στα δυο τμήματα a, b, έτσι ώστε  ο λόγος του αθροίσματος τους a+b προς τη μεγαλύτερη ποσότητα είναι ίσος με το λόγο της μεγαλύτερης ποσότητας προς τη μικρότερη.

Ο λόγος αυτός λέγεται «χρυσός λόγος» και σύμφωνα με τον ορισμό του Ευκλείδη, υπολογίζεται ότι έχει αριθμητική τιμή 1,618..., δηλαδή ότι το μεγαλύτερο τμήμα θα έχει πάντα 1,618... φορές μεγαλύτερο μήκος από το μικρότερο. 

ΧΡΥΣΟ ΟΡΘΟΓΩΝΙΟ ΚΑΙ ΧΡΥΣΗ ΕΛΙΚΑ

Ένα ορθογώνιο παραλληλόγραμμο λέγεται «χρυσό», όταν το πηλίκο της μεγαλύτερης προς τη μικρότερη πλευρά του ισούται με φ. 

Αυτό το ορθογώνιο έχει μια ιδιότητα που το ξεχωρίζει από όλα τα άλλα: αν αφαιρέσουμε από τη μια πλευρά το μεγαλύτερο δυνατό τετράγωνο, απομένει ένα καινούργιο ορθογώνιο, που είναι επίσης χρυσό, και αυτό μπορεί να συνεχιστεί επ’ άπειρον. 

Αν ενώσει κανείς με μια καμπύλη τις κορυφές όλων αυτών των ορθογωνίων, που είναι και χρυσές τομές, σχηματίζεται μια λογαριθμική έλικα, η «χρυσή έλικα».

Αν θέλει κανείς να δει ένα χρυσό ορθογώνιο αρκεί να κοιτάξει μια πιστωτική κάρτα, το σχήμα της οποίας είναι ακριβώς αυτό. 

ΧΡΥΣΟ ΤΡΙΓΩΝΟ

Χρυσό λέγεται κάθε ισοσκελές  τρίγωνο στο οποίο ο λόγος της μεγάλης πλευράς προς τη μικρή θα είναι ίσος με φ. Κάθε ισοσκελές με γωνία κορυφής 36˚ είναι χρυσό.

ΤΟ ΣΥΜΒΟΛΟ ΤΩΝ ΠΥΘΑΓΟΡΕΙΩΝ

Η χρυσή αναλογία ήταν γνωστή στους Πυθαγορείους. Το σύμβολο της αδελφότητας των Πυθαγορείων ήταν το «πεντάγραμμο» ή «πεντάλφα», το αστέρι δηλαδή που σχηματίζεται από τις πέντε διαγωνίους του κανονικού πενταγώνου. Η χρυσή αναλογία εμφανίζεται στις πλευρές του αστεριού. 

Αποδεικνύεται ότι κάθε πλευρά του «πενταγράμμου» διαιρεί τις δύο άλλες σε χρυσή τομή.

Ακόμη, το πηλίκο του εμβαδού του κανονικού πενταγώνου με κορυφές τις άκρες της πεντάλφα προς το εμβαδόν του κανονικού πενταγώνου που σχηματίζεται εντός του αστεριού ισούται με φ.

ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΗΣ ΑΝΑΠΑΡΑΓΩΓΗΣ ΤΩΝ ΚΟΥΝΕΛΙΩΝ

Ο Leonardo Pisano Fibonacci (1170-1240) γεννήθηκε στην Πίζα. Ο πατέρας του Leonardo, Guilielmo Bonacci, ήταν γραμματέας της Δημοκρατίας της Πίζας στη Βορειοαφρικανική πόλη Bugia. Ο Fibonacci μεγάλωσε εκεί και η εκπαίδευσή του επηρεάστηκε σημαντικά από τους Μαυριτανούς αλλά και από τα ταξίδια που έκανε αργότερα κατά μήκος της Μεσογειακής ακτής (Αίγυπτο, Συρία, Ελλάδα, Σικελία και Προβηγκία). Έτσι, μελέτησε και έμαθε τις μαθηματικές τεχνικές και τα αριθμητικά συστήματα που είχαν υιοθετηθεί σε εκείνες τις περιοχές.

Γύρω στο 1200, ο Fibonacci επέστρεψε στην Πίζα, όπου για τα επόμενα 25 χρόνια επεξεργαζόταν τις δικές του μαθηματικές συνθέσεις. Στο βιβλίο του με τίτλο "Liber Abaci",  εισήγαγε την έννοια της ακολουθίας στα Μαθηματικά της Δυτικής Ευρώπης. Σ’ έναν περίφημο, πλέον, συλλογισμό, προσπάθησε να υπολογίσει την ταχύτητα αναπαραγωγής των κουνελιών στη γη, κάτω από ιδανικές συνθήκες. Ο Fibonacci υπέθεσε ότι έχουμε 1 ζευγάρι κουνελιών, το οποίο αρχίζει να αναπαράγεται από τον πρώτο μήνα και μετά από κάθε μήνα κύησης, φέρνει στον κόσμο ένα ακόμη ζευγάρι. Κάθε νέο ζευγάρι είναι έτοιμο να τεκνοποιήσει 1 μήνα μετά τη γέννησή του, γεννά 1 μήνα μετά και συνεχίζει να αναπαράγεται με τον ίδιο ρυθμό. Πόσα ζευγάρια κουνελιών θα έχουμε στο τέλος του πρώτου χρόνου;

1. Αρχικά υπάρχει ένα ζευγάρι κουνελιών.
2. Στο τέλος του 1ου μήνα το αρχικό ζευγάρι είναι έτοιμο να ζευγαρώσει, αλλά υπάρχει μόνο αυτό.
3. Στο τέλος του 2ου μήνα έχουμε το αρχικό ζευγάρι και το πρώτο ζευγάρι παιδιών του. Συνολικά 2 ζευγάρια κουνελιών. 
4. Στο τέλος του 3ου μήνα έχουμε το αρχικό ζευγάρι, το πρώτο ζευγάρι παιδιών του, (που είναι έτοιμα κι αυτά να τεκνοποιήσουν) και ένα δεύτερο ζευγάρι παιδιών του. Συνολικά 3 ζευγάρια κουνελιών. 
5. Στο τέλος του 4ου μήνα έχουμε το αρχικό ζευγάρι, το πρώτο ζευγάρι παιδιών και το πρώτο δικό του ζευγάρι παιδιών, το δεύτερο ζευγάρι παιδιών, που είναι έτοιμα να τεκνοποιήσουν, και ένα νέο, τρίτο ζευγάρι παιδιών. Συνολικά 5 ζευγάρια κουνελιών. 

Με βάση αυτή την υπόθεση, ο Fibonacci ανακάλυψε ότι τα ζευγάρια των κουνελιών αυξάνονταν κάθε μήνα σύμφωνα με μια άπειρη ακολουθία αριθμών: 
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 114, 233, 377, 610...

Μπορείτε να εντοπίσετε το μοτίβο που κρύβεται πίσω από αυτή την αλληλουχία; 

Οι αριθμοί αυτοί ονομάστηκαν «αριθμοί Fibonacci» και αποτελούν τη λεγόμενη «Ακολουθία Fibonacci». Εκτός από τους δύο πρώτους αριθμούς που είναι το 1, κάθε αριθμός της ακολουθίας Fibonacci ισούται με το άθροισμα των δύο προηγουμένων: 

α_ν+2 = α_ν+1 + α_ν

Αν και υπάρχουν αναφορές ότι αυτή η ακολουθία είχε αναφερθεί περίπου μισό αιώνα πριν, από τους Ινδούς Gospala και Hemachandra, ο Fibonacci συνάντησε αυτή την ακολουθία μελετώντας την Μεγάλη Πυραμίδα του Χέοπα στην Αίγυπτο, η οποία και είναι χτισμένη με βάση τον αριθμό  φ.

Όμως, τι σχέση έχει η ακολουθία Fibonacci με το χρυσό αριθμό; 

Κατασκευάζουμε μια ακολουθία με τους λόγους των διαδοχικών όρων της ακολουθίας Fibonacci.

Μπορούμε να πάρουμε ένα κομπιουτεράκι και να κάνουμε τις διαιρέσεις. Θα διαπιστώσουμε πως όσο προχωράμε στην ακολουθία, το πηλίκο θα προσεγγίζει όλο και περισσότερο τον αριθμό φ.

π.χ.
5/3=1,66666666...
89/55=1,6181818...
377/233=1,618025751
987/610=1,618032787
46368/28657=1,618033988

Σε μαθηματικούς όρους, αυτό σημαίνει πως η ακολουθία των λόγων δύο διαδοχικών αριθμών Fibonacci έχει ως όριο τον αριθμό φ. Το συμπέρασμα αυτό αποδείχτηκε από τον μαθηματικό Robert Simpson το 1753, δηλαδή πεντέμιση αιώνες αργότερα από τον ορισμό της ακολουθίας από τον Fibonacci!

Εμβαθύνοντας λίγο στην Ανάλυση...

Όπως κάθε ακολουθία που προσδιορίζεται από αναδρομική σχέση, έτσι και η ακολουθία Fibonacci έχει έναν τύπο κλειστής μορφής, δηλαδή έναν γενικό τύπο που δίνει τον ν-οστό όρο. Αυτός είναι γνωστός ως τύπος του Binet:

Υπολογίζεται το όριο της ακολουθίας των λόγων δύο διαδοχικών όρων της F(n):

Παρόμοια, οι αριθμοί Fibonacci προσεγγίζουν εντυπωσιακά και τη χρυσή έλικα. Παρακάτω βλέπουμε μια κάλυψη του επιπέδου με τετράγωνα, οι πλευρές των οποίων είναι διαδοχικοί αριθμοί Fibonacci.

Ενώνουμε κάθε φορά δύο απέναντι κορυφές των τετραγώνων γράφοντας τόξα κύκλων. Σχηματίζεται η έλικα (ή σπείρα) Fibonacci, η οποία αποτελεί προσέγγιση της χρυσής έλικας. 

Η χρυσή αναλογία συνδέεται, δηλαδή, με τον πολλαπλασιασμό των κουνελιών, παρόλο που η Ακολουθία Fibonacci σχηματίστηκε ανεξάρτητα από την ευκλείδεια γεωμετρία. 

Ο φ ΚΑΙ Η ΑΛΓΕΒΡΑ

• Υπολογισμός του φ:

Για να υπολογίσουμε την τιμή του φ, ξεκινάμε από τον ορισμό:

Απλοποιώντας το αριστερό κλάσμα και αντικαθιστώντας το b/a = 1/φ, παίρνουμε

άρα,

Πολλαπλασιάζοντας και τα δύο μέλη με φ, παίρνουμε: φ + 1 = φ²

επομένως προκύπτει η εξίσωση: φ² – φ – 1 = 0

Χρησιμοποιώντας τη μέθοδο επίλυσης εξισώσεων 2^ου βαθμού, με διακρίνουσα, βρίσκουμε:

Επειδή το φ εκφράζει αναλογία μεταξύ θετικών ποσοτήτων, το φ είναι αναγκαστικά θετικό:

• Ιδιότητες:

1) Αν ελαττώσουμε τον φ κατά 1 μονάδα, αντιστρέφεται!

Επειδή φ = 1 + 1/φ , προκύπτει ότι 

2) Αν υψώσουμε τον φ στο τετράγωνο, αυξάνεται κατά 1 μονάδα!

Επειδή φ² = 1 + φ, παίρνουμε 

και αυτό μπορεί να συνεχιστεί επ’ άπειρον.

3) Ακόμα, για τον αριθμό φ ισχύει ότι:

• φ = 1φ
• φ² = 1φ + 1
• φ³ = 2φ + 1
• φ⁴ = 3φ + 2
• φ⁵ = 5φ + 3
• φ⁶ = 8φ + 5 …

Παρατηρούμε, δηλαδή, ότι στις δυνάμεις του φ «κρύβεται» η ακολουθία Fibonacci!

Η παραπάνω έκφραση μπορεί να χρησιμοποιηθεί για την ανάλυση μεγάλων δυνάμεων φⁿ σε έναν γραμμικό συνδυασμό του φ και του 1. Η σχέση που προκύπτει παράγει αριθμούς Fibonacci ως γραμμικούς συντελεστές:

φⁿ =  F(n) φ + F(n-1)

4) Μια άλλη έκφραση του αριθμού φ βασισμένη μόνο στο ψηφίο του 5 είναι η παρακάτω και οφείλεται στον Erol Karazincir:

ΠΑΝΤΑΧΟΥ ΠΑΡΩΝ…

Το Σύμπαν δείχνει να τρέφει μια ιδιαίτερη αδυναμία για τον αριθμό φ με τα άπειρα δεκαδικά ψηφία. 

(Συνεχίζεται...)

Πηγές:

Περιοδικό Focus

goldennumber.net

wikipedia.org
Πανεπιστημιακές σημειώσεις "Ευκλείδεια και μη Ευκλείδειες Γεωμετρίες" καθηγητή Χρ.Μπαϊκούση, 2011

Εν όψει των εξετάσεων...

Καλή επιτυχία στα παιδιά μας που δίνουν εξετάσεις!!! Παιδιά, κάντε συστηματικά την επανάληψή σας, χωρίς να κόψετε εντελώς τις βόλτες σας, γιατί τα πάντα χρειάζονται ένα πρόγραμμα! Και όταν γράφετε Μαθηματικά, προσοχή στις απλοποιήσεις! Να ξέρετε πως...

Σύνθετο... φρουτο-κουίζ!

1. Βρίσκουμε τον αριθμό στη θέση του λεμονιού
2. Βρίσκουμε τον αριθμό στη θέση του μήλου
3. Βρίσκουμε τον αριθμό στη θέση του πορτοκαλιού
4. Βρίσκουμε τον αριθμό στη θέση του ερωτηματικού!

(Πηγή) 

Αφήστε σχόλιο με τον αριθμό που βρήκατε... Η λύση θα δοθεί σύντομα!!!
  

Τα Μαθηματικά στην Τέχνη: Υπερβολή

Μαθαίνουμε για την υπερβολή μέσα από έργα τέχνης...

Josh Hufford (Σύγχρονος καλλιτέχνης) - "Within The Emptiness: Hyperbola"

Mary Rouncefield (Σύγχρονη καλλιτέχνιδα) - "Hyperbola"

Slav Nedev (Σύγχρονος καλλιτέχνης) - "Y=f(x)" (1995)

Τα βιβλία γράφουν...

Έστω Ε και Ε΄ δύο σημεία του επιπέδου. Ονομάζεται υπερβολή με εστίες τα σημεία Ε και Ε΄ ο γεωμετρικός τόπος C των σημείων του επιπέδου, των οποίων η απόλυτη τιμή της διαφοράς των αποστάσεων από τα Ε και Ε΄ είναι σταθερή και μικρότερη του Ε΄Ε. Η απόσταση Ε΄Ε ονομάζεται εστιακή απόσταση της υπερβολής.

Russell Kightley (Σύγχρονος καλλιτέχνης) - "Hyperbola"

Τα βιβλία επίσης γράφουν...

Η υπερβολή μπορεί να προκύψει από την τομή ενός κώνου με ένα επίπεδο, γι' αυτό και είναι μία από τις κωνικές τομές. 

.*.〰.*.〰.*.〰.*.〰.*.〰.*.〰.*.

"O πίνακας ζωγραφικής "Y=f(x)" δημιουργήθηκε με τη βοήθεια ενός μαθηματικού τύπου, συγκεκριμένα της συνάρτησης y=1/x. H καμπύλη που προκύπτει είναι μια υπερβολή. Η άλλη αρχή που χρησιμοποιήθηκε είναι αυτή της χρυσής τομής. Ήταν ενδιαφέρον να πειραματιστώ, θέλοντας να δείξω πώς μια μαθηματική έκφραση μπορεί επίσης να έχει αισθητική. Τα Μαθηματικά είναι παντού γύρω μας και μας πληροφορούν για την όλη ύπαρξη".
Slav Nedev

.*.〰.*.〰.*.〰.*.〰.*.〰.*.〰.*.

Πηγές:

• Μαθηματικά Θετικής και Τεχνολογικής Κατεύθυνσης Β' Γενικού Λυκείου, ΟΕΔΒ, 2003
• Θ. Κουφογιώργος, Μαθήματα Αναλυτικής Γεωμετρίας, Τυπογραφείο Πανεπιστημίου Ιωαννίνων, 2004
• E.H. Gombrich, Το Χρονικό της Τέχνης, Μορφωτικό Ίδρυμα Εθνικής Τραπέζης, 1995
• Wassily Kandinsky, Σημείο-Γραμμή-Επίπεδο, Εκδόσεις Δωδώνη, 2013
• Wassily Kandinsky, Για το πνευματικό στην Τέχνη, Εκδόσεις Νεφέλη, 1981
• H.L.C Jaffe, Η ζωγραφική στον 20ό αιώνα, Εκδόσεις Νεφέλη, 1984
• Deviant Art: Josh Hufford 
• Fine Art America: Hyperbola
• Mary Rouncefield
• Saatchi Art: Slav Nedev
• wikipedia.org

Τα Μαθηματικά στην Τέχνη: Παραβολή

Μαθαίνουμε για την παραβολή μέσα από έργα τέχνης...

Josh Hufford (Σύγχρονος καλλιτέχνης) - "This Holy Reality-Parabola"

Jutta Maria Pusl (Σύγχρονη καλλιτέχνιδα) - "Parabolic"

Mary Rouncefield (Σύγχρονη καλλιτέχνιδα) - "Confined"

Mary Rouncefield (Σύγχρονη καλλιτέχνιδα) - "Area"

Τα βιβλία γράφουν...

Έστω μια ευθεία δ και ένα σημείο Ε εκτός της δ. Ονομάζεται παραβολή με εστία το σημείο Ε και διευθετούσα την ευθεία δ ο γεωμετρικός τόπος C των σημείων του επιπέδου τα οποία ισαπέχουν από την Ε και τη δ. Αν Α είναι η προβολή της εστίας Ε στη διευθετούσα δ, τότε το μέσο Κ του ΕΑ είναι προφανώς σημείο της παραβολής και λέγεται κορυφή της.

Russell Kightley (Σύγχρονος καλλιτέχνης) - "Parabola"

Τα βιβλία επίσης γράφουν...

Η παραβολή μπορεί να προκύψει από την τομή ενός κώνου με ένα επίπεδο, γι' αυτό και είναι μία από τις κωνικές τομές. 

Πηγές:

• Μαθηματικά Θετικής και Τεχνολογικής Κατεύθυνσης Β' Γενικού Λυκείου, ΟΕΔΒ, 2003
• Θ. Κουφογιώργος, Μαθήματα Αναλυτικής Γεωμετρίας, Τυπογραφείο Πανεπιστημίου Ιωαννίνων, 2004
• E.H. Gombrich, Το Χρονικό της Τέχνης, Μορφωτικό Ίδρυμα Εθνικής Τραπέζης, 1995
• Wassily Kandinsky, Σημείο-Γραμμή-Επίπεδο, Εκδόσεις Δωδώνη, 2013
• Wassily Kandinsky, Για το πνευματικό στην Τέχνη, Εκδόσεις Νεφέλη, 1981
• H.L.C Jaffe, Η ζωγραφική στον 20ό αιώνα, Εκδόσεις Νεφέλη, 1984
• Deviant Art: Josh Hufford 
• Fine Art America: Jutta Maria Pusl
• Pixels: Russell Kightley
• Mary Rouncefield
• wikipedia.org

Μετρώντας τη Γη: Ο μεγαλοφυής υπολογισμός του Ερατοσθένη

Η πρώτη φορά στην ιστορία κατά την οποία έγινε πραγματική μέτρηση για τον υπολογισμό της περιμέτρου της Γης, ήταν από τον Ερατοσθένη τον Κυρηναίο (276 πΧ – 194 πΧ), ο οποίος υπολόγισε με εκπληκτική ακρίβεια την περίμετρο της Γης από... ένα πηγάδι. Για τη μέτρηση αυτή ο Ερατοσθένης είχε γράψει ιδιαίτερη πραγματεία, όπως πληροφορούμαστε από την «Διόπτρα» του Ήρωνος του Αλεξανδρέως, ο οποίος αναφερόμενος στο μέγεθος της περιμέτρου της Γης σημειώνει: «Ερατοσθένης εν τω επιγραφομένω περί αναμετρήσεως της Γης».

Ο Ερατοσθένης γεννήθηκε στην ελληνική αποικία της Βόρειας Αφρικής, Κυρήνη και ήταν φίλος με τον Αρχιμήδη. Λέγεται ότι είχε ζήσει στην Αθήνα για αρκετά χρόνια, ώσπου έγινε βιβλιοθηκάριος στην περίφημη βιβλιοθήκη της Αλεξάνδρειας, όπου και μελετούσε.

Πώς ένα πηγάδι βοήθησε τον Ερατοσθένη να αποδείξει ότι η Γη είναι στρογγυλή...

Η άποψη ότι η Γη ήταν σφαιρική ήταν αποδεκτή στην αρχαία Ελλάδα. Ο Ερατοσθένης ήταν εκείνος που απέδειξε μαθηματικά αυτή την πεποίθηση και μάλιστα υπολόγισε με αξιοθαύμαστη ακρίβεια την ακτίνα και την περίμετρο της σφαιρικής Γης.

Την εποχή που βρισκόταν στη βιβλιοθήκη, ο Ερατοσθένης πληροφορήθηκε για ένα πολύ περίεργο πηγάδι, το οποίο βρισκόταν κοντά στη Συήνη (σημερινό Ασουάν της νότιας Αιγύπτου). Κάθε χρόνο, το μεσημέρι της 21ης Ιουνίου - τη μέρα του θερινού ηλιοστασίου, δηλαδή τη μεγαλύτερη μέρα του έτους - ο Ήλιος καθρεφτιζόταν ολόκληρος μέσα στο πηγάδι και το φώτιζε μέχρι τον πυθμένα του, χωρίς να δημιουργείται σκιά γύρω από αυτό. Ο Ερατοσθένης συμπέρανε ότι για να συμβαίνει κάτι τέτοιο, τη συγκεκριμένη μέρα ο Ήλιος έπρεπε να βρίσκεται ακριβώς κατακόρυφα πάνω από το πηγάδι.

Ο ήλιος όμως δεν συμπεριφερόταν το ίδιο και στα βόρεια της Αιγύπτου. Στην Αλεξάνδρεια, η οποία απέχει 800 χλμ από το Ασουάν, την ίδια εκείνη μέρα, ο ήλιος δημιουργούσε μια μικρή σκιά σε μια ψηλή κολώνα. Αυτό σήμαινε ότι οι δύο πόλεις σίγουρα δεν έβλεπαν τον ήλιο υπό την ίδια γωνία. Ο Ερατοσθένης γνώριζε ήδη από προγενέστερες αστρολογικές μετρήσεις που διάβασε στη βιβλιοθήκη ή από δικούς του υπολογισμούς, ότι η Συήνη και η Αλεξάνδρεια ανήκαν στον ίδιο μεσημβρινό. Επομένως ο λόγος που ο Ήλιος δεν μπορούσε να μεσουρανεί ταυτόχρονα στη Συήνη και στην Αλεξάνδρεια οφειλόταν στο ότι η Γη ήταν στρογγυλή και όχι επίπεδη. 

Πώς ο Ερατοσθένης υπολόγισε την περίμετρο της Γης...

Το πείραμα του Ερατοσθένη βασίστηκε στη μέτρηση της γωνίας υπό την οποία ο Ήλιος έστελνε τις ακτίνες του σε δύο διαφορετικές τοποθεσίες (Αλεξάνδρεια και Συήνη), την ίδια χρονική στιγμή.  Ο Ερατοσθένης πραγματοποίησε το πείραμα στις 21 Ιουνίου, την ημέρα του θερινού ηλιοστασίου, όταν η Γη παρουσιάζει τη μέγιστη κλίση της ως προς τον Ήλιο. Αυτό σημαίνει ότι ο Ήλιος το μεσημέρι βρισκόταν ακριβώς πάνω από τις δύο πόλεις.

Στο σχήμα βλέπουμε παράλληλες ακτίνες να φτάνουν από τον Ήλιο στη Γη. Το μεσημέρι της 21^ης Ιουνίου, οι ηλιακές ακτίνες βυθίζονται στο πηγάδι της Συήνης, χωρίς να δημιουργούν καμία σκιά, επομένως «κατευθύνονται» προς το κέντρο της Γης. 

Την ίδια χρονική στιγμή στην Αλεξάνδρεια, μία ψηλή κολώνα (κάθετη στο έδαφος) σχηματίζει μια μικρή σκιά. Ο Ερατοσθένης μέτρησε το ύψος της κολώνας και το μήκος της σκιάς της. Έτσι δημιούργησε ένα ορθογώνιο τρίγωνο και, χρησιμοποιώντας την τριγωνομετρία, υπολόγισε τη γωνία που σχηματιζόταν ανάμεσα στην κολώνα και στις ακτίνες του Ήλιου. Το αποτέλεσμα ήταν ότι η γωνία ήταν φ = 7,2˚ , δηλαδή το 1/50 της περιφέρειας του κύκλου που είναι 360˚.

Εδώ έχει μεγάλη σημασία το ότι η γωνία φ ισούται με τη γωνία που σχηματίζεται ανάμεσα στις δύο ακτίνες που συνδέουν το κέντρο της Γης με την Αλεξάνδρεια και τη Συήνη αντίστοιχα (εντός εναλλάξ γωνίες).

Στη συνέχεια, με την βοήθεια του βασιλιά Πτολεμαίου, ο οποίος διέθεσε ένα είδος οδομέτρου με γρανάζια, μέτρησε την απόσταση των δύο πόλεων, που ήταν 5.040 στάδια. Στο πείραμα του, τα 5.040 στάδια αντιστοιχούσαν στο 1/50 της περιφέρειας του κύκλου.

Τέλος, πολλαπλασίασε το 5.040 με το 100% του κύκλου, δηλαδή το 50, και έτσι υπολόγισε την περίμετρο της Γης στα 252.000 στάδια, ή με τη σύγχρονη μονάδα μέτρησης, 39.690 χιλιόμετρα. Ο υπολογισμός που έκανε ο Ερατοσθένης 2.200 χρόνια πριν ήταν αρκετά ακριβής. Σήμερα η περίμετρος της Γης υπολογίζεται σύμφωνα με δορυφορικές μετρήσεις σε 40.048 χιλιόμετρα, άρα στην ουσία έπεσε έξω μόλις 358 χιλιόμετρα!

Πηγες:

Τζόνι Μπολ, Μαθημαγικά, Εκδόσεις Polaris, 2011

wikipedia.org