"Παράλληλοι Κόσμοι"

Οι «Παράλληλοι Κόσμοι» είναι ένα διαστημικό ταξίδι στα πέρατα της φαντασίας, στις μαύρες τρύπες, στις χρονομηχανές, στα εναλλακτικά σύμπαντα και τον πολυδιάστατο χώρο. Είναι ένα εκθαμβωτικό πορτρέτο της θυελλώδους επανάστασης που σαρώνει το τοπίο της σημερινής κοσμολογίας. Το Σύμπαν μας μοιάζει με κοσμική φυσαλίδα που αναδεύεται αιώνια μέσα σε έναν ωκεανό από σύμπαντα-φυσαλίδες. Ποια είναι η μοίρα της; Μήπως η εξαφάνισή της σημάνει το τέλος του δικού μας Σύμπαντος; Γύρω της - σε απόσταση χιλιοστών - γίνονται συνεχώς Μεγάλες Εκρήξεις, μέσα από τις οποίες γεννιούνται νέα, παράλληλα (με το δικό μας) σύμπαντα. Άραγε, μετά από δισεκατομμύρια χρόνια - εκείνη τη μακάβρια εποχή - λίγο πριν το Σύμπαν μας καταλήξει, ψυχρό και σκοτεινό, στο παντοτινό τέλος του, θα μπορούσε η ανθρωπότητα να διαιωνίσει την ύπαρξή της μετοικώντας σε ένα άλλο, γειτονικό σύμπαν; Η ιδέα των παράλληλων Κόσμων και η θεωρία χορδών που ερμηνεύει την ύπαρξή τους αντιμετωπίζονταν κάποτε με καχυποψία, ενώ οι επιστήμονες που την υπερασπίζονταν θεωρούνταν μυστικιστές, τρελοί ή τσαρλατάνοι. Σήμερα, οι φυσικοί την υποστηρίζουν με πάθος και μάλιστα υιοθετούν την πρόσφατη εκδοχή της, τη θεωρία-Μ, ως τη μόνη σωστή θεωρία, την πιο κομψή και απλή απάντηση στο ύψιστο ερώτημα: «Τι υπήρχε πριν από το Big Bang;»

Μαθηματικά στην τηλεόραση: "The Big Bang Theory"

📺Στην προσπάθεια να συγκεντρώσουμε τις καλύτερες τηλεοπτικές σειρές με μαθηματικό περιεχόμενο, η σειρά που έχει σήμερα την τιμητική της είναι η πολυαγαπημένη “The Big Bang Theory”…

 

🎞️Πρώτη κυκλοφορία: 2007

🎥Σεζόν: 12

📜Υπόθεση:

Ο Leonard και ο Sheldon, δύο λαμπροί, εκκεντρικοί φυσικοί που εργάζονται στο Cal Τech της Καλιφόρνια, είναι, εκτός από συνάδελφοι, συγκάτοικοι και κολλητοί φίλοι. Οι δύο άλλοι φίλοι τους και συνάδελφοι από το Cal Τech, Howard και Raj, συμπληρώνουν την εκκεντρική, nerdy τετράδα. Καθώς όλοι τους είναι «βυθισμένοι» στην επιστημονική τους έρευνα, αλλά και σε βιντεοπαιχνίδια, κόμικς και ταινίες επιστημονικής φαντασίας, δεν φαίνεται να έχουν μεγάλη τύχη όσον αφορά το αντίθετο φύλο. Όλα αλλάζουν όταν απέναντι από το διαμέρισμα των Leonard και Sheldon μετακομίζει η πανέμορφη σερβιτόρα και επίδοξη ηθοποιός Penny…

Σε μια σειρά με πρωταγωνιστές τέσσερις φυσικούς, τα μαθηματικά αναπόφευκτα κάνουν την εμφάνισή τους. Η σειρά έχει εμπνεύσει ακόμη και μια μαθηματική απόδειξη! Σε ένα επεισόδιο, ο Sheldon είπε ότι ο αγαπημένος του αριθμός ήταν το 73. Γιατί; Το 73 είναι ο 21^ος πρώτος αριθμός. Τώρα, αναστρέφοντας το 21 παίρνουμε τον αριθμό 12. Ποιος είναι ο 12^ος πρώτος αριθμός; Το 37, που είναι, φυσικά, το 73 ανεστραμμένο. Ενώ το 21 από την άλλη ισούται με 3 επί 7. Ανάλογες ιδιότητες έχει και στο δυαδικό σύστημα! 

 

Ο καθηγητής του Κολλεγίου Dartmouth και φαν της εκπομπής, Carl Pomerance, ήταν περίεργος για το αν αυτή ήταν η μόνη περίπτωση στην οποία αυτό ήταν δυνατό ή όχι και έγραψε μια απόδειξη για το θέμα, που έχει ονομαστεί ανεπίσημα «Η εικασία του Sheldon». Ένα τμήμα της απόδειξης εμφανίστηκε ακόμη και στο παρασκήνιο του επεισοδίου με τίτλο “The Inspiration Deprivation”. Την απόδειξη μπορείτε να διαβάσετε εδώ. 

Ο Sheldon χρησιμοποιεί το Θεώρημα του Bayes

💡Ιδέα που πρεσβεύει: “Smart is the new sexy”.

💬Γράψτε στα σχόλια, όσοι έχετε δει τη σειρά, τη γνώμη σας. Ποιες άλλες σειρές με μαθηματικό περιεχόμενο έχετε να προτείνετε;

🎬Τσεκάρετε εδώ τη λίστα με τις μαθηματικές ταινίες που έχουμε συγκεντρώσει.

Ο χαρταετός!

 

Γράφει ο Αθ. Δ. Γκίκας, Μαθηματικός

Δημήτρης Μυταράς (1934-2017) - "Χαρταετοί"

 

Κάποιες ατέλειωτες νύχτες φέρνω πίσω από τα πέλαγα του χρόνου τα βιώματά μου τα παλιά και ακούραστα. Τα βιώματά μου είναι η μαγιά για το κείμενο που ακολουθεί. Λες πάντα καλύτερα την ιστορία που έχεις κατακτήσει. Αν δεν έχεις τα βιώματα δεν έχεις τίποτα. Τα αληθινότερα κείμενα είναι εκείνα που έχουν αφετηρία τον εαυτό μας. Θα επιχειρήσω να εξισορροπήσω την αλήθεια με την αναγνωσιμότητα.
Έθιμο της Καθαράς Δευτέρας είναι το πέταγμα του χαρταετού. Η οικογένεια αφού επιβιβαστεί στο αυτοκίνητό της, πάρει και τα απαραίτητα φαγώσιμα, θα σταματήσει στο κοντινό περίπτερο ν’ αγοράσει το χαρταετό, έτσι για να διατηρηθεί το έθιμο. Ποιο χαρταετό θα μου πείτε; Αυτόν με τις φιγούρες από σύγχρονα κόμικς στην επιφάνειά του ή με σήμα κάποιας ποδοσφαιρικής ομάδας. Και αφού πάνε στην εξοχή θ’ αρχίσει η διαδικασία το πετάγματος πλην ματαίως, τις περισσότερες φορές.

Η σκηνή σαν και τούτη:

-  Ο μικρός θα γκρινιάζει γιατί ο δικός του δεν «σηκώθηκε».
- Ο πατέρας μπλεγμένος μες στους σπάγγους και το ξερόχορτο θα ρίχνει τις ευθύνες στη μητέρα γιατί δεν του έκανε καλό «κεφάλι».
-     Όταν ξεμπλέξει με το λιγοστό σπάγγο που θα του έχει απομείνει θα τρέχει σαν τρελλός στα χωράφια για να πάρει λίγο ύψος ο αετός. Ύστερα περήφανος θα εξομολογείται:  Τον «σήκωσα» και φέτος !

Σπύρος Βασιλείου (1903-1985) - "Τα σαρακοστιανά" (1950)

Η ημέρα θα κυλίσει με άριστες επιδόσεις στην κατανάλωση λαγάνας, ταραμοσαλάτας, καλαμαριών καβουριών και άλλων «σαρακοστιανών» και περιχαρείς θα επιστρέψουν στο σπίτι. Περιχαρείς; Όλο και κάποιοι θα νοιώθουν εκείνο το κενό μέσα τους, το ονομαζόμενο «μεθεόρτιο σύνδρομο» από τους ψυχολόγους, που προέρχεται από τις πολλές ελπίδες που είχαν στηρίξει στην Καθαροδευτεριάτικη έξοδο και δεν επαληθεύτηκαν.
Και πώς να μην γίνει έτσι. Πόσο κοπίασαν για τον αετό; Τί ξέρουν για το σκελετό του με τα «ψυχοκάλαμα» ; Πόσο κοπίασαν για τα ζύγια του; Ας είναι καλά οι πήχες από το ξυλουργείο κι η βιοτεχνία που φτιάχνει αετούς χωρίς «ψυχή»; Πώς ν’ ασχοληθείς με το πέταγμα, αφού δεν καταπιάστηκες ποτέ με την κατασκευή του και μέσα από αυτή, διδάσκοντας την στα παιδιά σου, να δίνεις και να παίρνεις και συ χαρά; Χωρίς περιστροφές θα πω ότι τα πράγματα στις ημέρες μου ήταν καλύτερα. Τούτο όχι από συνήθεια που έχουμε οι παλιότεροι να ωραιοποιούμε καταστάσεις που ζήσαμε… και τότε δεν ήταν όλα ωραία. Άλλα πράγματα ήταν χειρότερα από σήμερα.
Όμως επειδή ο λόγος πρέπει να είναι «ορθός αποδεικτικός», όπως στα ΜΑΘΗΜΑΤΙΚΑ, θα επιχειρήσω τη σύγκριση κι ας βγάλει ο αναγνώστης τα συμπεράσματά του.

Πρώτα πρώτα για μας το πέταγμα του αετού δεν ήταν σαν το «στιγμιαίο αδίκημα» δηλ. αγοράζω την Κ. Δευτέρα το πρωί, κάνω προσπάθεια για πέταγμα και τελείωσα. Ήταν ολόκληρη ιεροτελεστία που άρχιζε μια δυο εβδομάδες πριν. Όταν είσαι νέος έχεις το χρόνο στο πλευρό σου ανεξάντλητο κα όλα είναι συναρπαστικά.

- Πρώτα τα καλάμια για το σκελετό. Ας ήταν καλά τα μαντριά προβάτων. Και σήμερα αν θέλει κάποιος μπορεί να βρει δίπλα σε  αυλάκια.
- Μετά τη φροντίδα για τις κόλλες, το ζυμάρι που θα τις κολλούσε.
- Ο σπάγγος ο κερωμένος για να κρατάει καλύτερα.
- Κουρέλια ή φύλλα από το κιντρινόχρωμο πρόχειρο σχολικό τετράδιο, για την ουρά. Βλέπεις δεν έφτανε η «δραχμή» ν’ αγοράσεις και δεύτερη κόλλα για τις φούντες της ουράς.

Τα δύσκολα άρχιζαν στην συναρμολόγηση. Πώς θα κατορθώσεις να φτιάξεις το κανονικό εξάγωνο. Το μυστικό πήγαινε από τα μεγαλύτερα παιδιά της παρέας στα μικρότερα έτσι εμπειρικά. Εγώ το διδάχτηκα από τον ξαδελφό μου Κ. Γκίκα γεωπόνο, που με τα μακριά και επιδέξια δάκτυλά του έκανε τους καλύτερους χαρταετούς. Θαύμαζα τους αετούς του. Σήμερα δε θαυμάζουμε αλλά θαμπωνόμαστε από ένα συμβάν επιτυχίας. Παλαιά υπήρχαν πρότυπα σε γειτονιές, στο σχολείο, στα αθλήματα, σε εργασιακούς χώρους, όπου μια δεξιότητα μας κέντριζε σε άμιλλα. Θαυμασμός εσωτερικός . ήταν αναμέτρηση με τους εαυτούς μας. Γιατί ο Κώστας φτιάχνει αετό και να μη μπορώ και γω! Έτσι όχι μόνο μαθαίναμε, αλλά συγχρόνως γινόμασταν καράβι που μετέφερε τη γνώση στο επόμενο λιμάνι της αρχέγονης αλυσίδας ζωής. Αν το φορτίο το παραδώσαμε σωστά, τότε η ζωή μας έχει νόημα.

Στην παρουσίαση της κατασκευής θα ακολουθήσω την αρχή της εποπτικότητας, με σκοπό διδακτικό, αισθητικό και κύρια τεκμηριωτικό. Αφού και τα τρία καλάμια ΑΔ, ΓΖ, ΒΕ κεντραριζόντουσαν στο μέσο Ο με καρφίτσα αρχικά για να μπορεί να περιστρέφονται, με την αρχή του σπάγγου στο σημείο Α μετρούσαμε μέχρι το Ο και δέναμε στο Β. Πάλι από το Β μετρούσαμε μέχρι το Ο και δέναμε στο Γ κ.λ.π. Έτσι το εξάγωνο ήταν έτοιμο. Έπρεπε να γίνω Μαθηματικός για να δώσω τη θεωρητική εξήγηση στην κατασκευή του κανονικού εξαγώνου μ’ αυτόν τον τρόπο που περιέγραψα.

 

 

Σχήμα του Αθ.Δ. Γκίκα με τα μαθηματικά του χαρταετού

 

Η εμπειρική κατασκευή στηρίζεται στην Μαθηματική αλήθεια ότι:
Η πλευρά του κανονικού εξαγώνου ΑΒ = ΑΟ = R = ακτίνα περιγεγραμμένου κύκλου.

Από την κατασκευή του αετού ξεκινούσα στη Β΄ Λυκείου την διδασκαλία του κανονικού εξαγώνου, έτσι όπως απαιτεί η διδακτική των Μαθηματικών από την εμπειρία στο θεωρητικό μοντέλο και αντίστροφα.

 

Στα πρώτα χρόνια υπήρχαν μαθητές, που βοηθούσαν στο πέρασμα από την εμπειρία στη θεωρία. Σιγά σιγά, όλο και λιγόστευαν, αφού κανένας γονιός δεν δίδαξε το παιδί του πώς να φτιάχνει αετό. Αν το είχε κάμει θα του είχε μάθει χωρίς καλά καλά να το καταλαβαίνει ο ίδιος και τις ιδιότητες του κανονικού εξαγώνου – θα φανεί παρακάτω του λόγου το ασφαλές. Ας έλθουμε στα ζύγια που πετάγματος ΚΑ, ΚΒ, ΚΟ και της ουράς ΛΕ, ΛΔ.

Σχεδόν πάντοτε όλα είχαν το ίδιο μήκος με την πλευρά (ακτίνα). Όμως, αν ήθελε κάποιος να παίρνει ύψος ο αετός του, κρατούσε το μεσιανό, το ΚΟ μικρότερο, όχι όσο αυτός ήθελε. Τα Μαθηματικά έχουν και πάλι το λόγο, όσο δηλ. το απόστημα ΟΘ του κανονικού εξαγώνου. Εφαρμόζοντας το Πυθαγόρειο Θεώρημα στο τρίγωνο ΟΓΘ θα βρείτε:

 \(ΟΘ=\frac{R \sqrt{3}}{2} \simeq 0,86R\)

 

Και επειδή η πλευρά του κανονικού εξαγώνου είναι όσο και η ακτίνα, το μεσαίο ζύγι είναι τα 0,86 πλευράς. Κατ’ αυτό τον τρόπο, ο αετός υψωνόταν σχεδόν κατακόρυφα, ο σπάγγος του δεν έκανε «κοιλιά», που δεν ήταν τίποτα άλλο από την αλυσοειδή καμπύλη της Θεωρητικής Μηχανικής.

Περιέγραψα την κατασκευή για να είναι η σύγκριση ευχερής. Εμάς μας γέμιζε πριν απ’ όλα η προετοιμασία. Το πέταγμα ήταν η κορύφωση. Νοιώθαμε έρωτα γι’ αυτόν. Τον μαθαίναμε και τον χορταίναμε κατασκευάζοντάς τον. Και όταν τον βλέπαμε να σηκώνεται στα ύψη νοιώθαμε περισσότερο ελεύθεροι. Νικούσαμε την βαρύτητα της Γής που μας κρατά καθηλωμένους χιλιάδες χρόνια πάνω της. Λίκνο του ανθρώπινου γένους και του πολιτισμού του η γη, αλλά και τα δεσμά του. Σαν τον υψώναμε ψηλά και η καλούμπα είχε φτάσει στο τέλος, του στέλναμε και ένα «μήνυμα» του αετού ! Τι ήταν το μήνυμα; Ένα στρογγυλό χαρτί με μια τρύπα στη μέση, συνήθως από το πακέτο τσιγάρων των θεριακλήδων της παρέας, που το περνούσαμε στο σπάγγο και ο αέρας το προχωρούσε μέχρι τον αετό! Έτσι με το πέταγμα το αετού περνούσαμε τις ελεύθερες ώρες σχεδόν όλο το σαρανταήμερο. Όσο κρατούσε το ανοιξιάτικο βοριαδάκι και μας το επέτρεπε. Μετά τον κρεμούσαμε στο υπόγειο, εφόσον δεν είχε καρφωθεί σε κανένα δένδρο. Σύρματα της Δ.Ε.Η. δεν υπήρχαν για εμπόδια και ηλεκτροπληξίες. Έφτιαξα αετούς για τα παιδιά μου, τα ανίψια μου και τον εγγονό μου.
Θα πει κάποιος: Αφού δίδαξες τα παιδιά σου, συ κατασκευάζεις και για το εγγόνι;
-  Ε! λοιπόν, ναι. Τα παιδιά δεν τα είδα αποφασισμένα να γονατίσουν στο πάτωμα και ν’ ανακατευτούν με κόλλες, ψαλίδια και σπάγγους. Τα είδα να κατευθύνονται στο γειτονικό περίπτερο!! Εγώ πάντως κάτι κερδίζω. Γίνομαι πάλι παιδί. Μόνο δυο φορές στη ζωή μας γινόμαστε παιδιά. Όταν είμαστε πραγματικά παιδιά και όντας μεγάλοι, να μπορούμε να κατακτήσουμε πάλι όσα μας έκαναν εντύπωση ως παιδιά. Η παιδική μνήμη είναι παντοδύναμη. Παραμένουμε ζωντανοί χάρη στην αυταξία ορισμένων στιγμών, που επιλέγουμε, δημιουργώντας μια δεύτερη ροή παράλληλη με τις ρυτίδες μας. 

 

Πηγή: Λαμιακός Τύπος

Αλέκος Φασιανός (1935-2022) - "Χαρταετός"

 

🌐Ένα αναλυτικό tutorial για την κατασκευή χαρταετού, καθώς και τη Φυσική που χρησιμεύει για το πέταγμα του χαρταετού, θα βρείτε στο ιστολόγιο Πειράματα Φυσικής με Απλά Υλικά.

 

Τα κρυμμένα μαθηματικά στην "Έναστρη Νύχτα" του van Gogh

 

Η «Έναστρη Νύχτα» του Vincent van Gogh είναι μια ελαιογραφία σε καμβά η οποία απεικονίζει μια θέα λίγο πριν την ανατολή του ηλίου από το ανατολικό παράθυρο του δωματίου του ασύλου όπου διέμενε ο καλλιτέχνης στο Saint-Rémy-de-Provence στη νότια Γαλλία. Ο βαν Γκογκ είχε  αυτοβούλως ζητήσει τον εγκλεισμό του στο άσυλο μετά τον αυτο-ακρωτηριασμό του αριστερού του αυτιού, τον Δεκέμβριο του 1888.

Εκτιθέμενη από το 1941 στο Μουσείο Μοντέρνας Τέχνης της Νέας Υόρκης, η «Έναστρη Νύχτα» είναι ένα εξαιρετικά δημοφιλές έργο τέχνης.

 

Το αστραφτερό φως των αστεριών και τα στροβιλιζόμενα σύννεφα στον πίνακα αυτό, πιστευόταν παλιότερα ότι αντανακλούν την ταραχώδη ψυχική κατάσταση του καλλιτέχνη όταν ζωγράφιζε το έργο την άνοιξη του 1889. Πλέον, μελέτες από φυσικούς επιστήμονες έχουν δείξει ότι ο καλλιτέχνης είχε μια βαθιά, διαισθητική κατανόηση της μαθηματικής δομής της τυρβώδους ροής.

 

Τι είναι η τυρβώδης ροή;

Η τυρβώδης ροή είναι ένα συγκεκριμένο είδος ροής των ρευστών που μέσα της σχηματίζονται στρόβιλοι. Ως συνηθισμένο φυσικό φαινόμενο που παρατηρείται στα ρευστά –κινούμενο νερό, ωκεάνια ρεύματα, ροή αίματος, ατμοσφαιρικό οριακό στρώμα, διογκούμενα σύννεφα καταιγίδας,  νέφη καπνού και καπνός από τσιγάρο– η τυρβώδης ροή είναι χαοτική, καθώς σχηματίζονται μικρότεροι στρόβιλοι μέσα σε μεγαλύτερους. Είναι κάτι που αποτελεί καθημερινή μας εμπειρία και πρόκληση αξεπέραστη για τους μαθηματικούς φυσικούς.

Μπορεί να φαίνεται τυχαίο στον περιστασιακό παρατηρητή, ωστόσο οι «αναταράξεις» ακολουθούν ένα διαδοχικό μοτίβο που μπορεί να μελετηθεί και, τουλάχιστον εν μέρει, να εξηγηθεί χρησιμοποιώντας μαθηματικές εξισώσεις.

Τα αστέρια του πίνακα, ο πλανήτης Αφροδίτη και το άστρο V838 Mon

«Μέσα από το παράθυρο με τα σιδερένια κάγκελα» γράφει ο Βαν Γκογκ στον αδελφό του Τεό, τον Μάιο του 1889, «μπορώ να διακρίνω ένα τετράγωνο κομμάτι γης με σιτάρι… πάνω από το οποίο, το πρωί, βλέπω τον ήλιο να ανατέλλει σε όλο του το μεγαλείο».

H «Έναστρη Νύχτα» είναι το μόνο νυχτερινό έργο στη σειρά πινάκων με τη θέα από το παράθυρο του υπνοδωματίου του. Στις αρχές Ιουνίου, έγραψε στον Τεό: «Σήμερα το πρωί είδα το τοπίο από το παράθυρό μου για μεγάλο χρονικό διάστημα πριν από την ανατολή με τίποτα άλλο εκτός από το πρωινό άστρο, το οποίο φάνταζε πολύ μεγάλο».

Οι ερευνητές έχουν καταλήξει στο συμπέρασμα ότι η Αφροδίτη ήταν πράγματι ορατή την αυγή, στην Προβηγκία, την άνοιξη του 1889 και την εποχή εκείνη ήταν κοντά στο φωτεινότερο δυνατό της. Έτσι, το πιο λαμπρό «αστέρι» στον πίνακα, δεξιά από το κυπαρίσσι, είναι στην πραγματικότητα η Αφροδίτη.

Μια φωτογραφία από το διαστημικό τηλεσκόπιο Hubble που δημοσιεύθηκε το 2004 έδειχνε ένα μακρινό άστρο, το V838 Mon στον αστερισμό Μονόκερως, να μοιάζει με τα άστρα της «Έναστρης Νύχτας» όπου ο Βαν Γκογκ φαντάζεται το φως τους να στροβιλίζεται. Στο άστρο V838 Mon, που βρίσκεται 20.000 έτη φωτός μακριά από τη Γη, οι φωτεινοί στροβιλισμοί οφείλονται στην σκόνη και στην τυρβώδη ροή των αερίων γύρω από αυτό.

Το 2006, οι ερευνητές J.L. Aragón, Gerardo G. Naumis, M. Bai, M. Torres και P.K. Maini, μετά την δημοσίευση της φωτογραφίας του Hubble, εξέτασαν την μαθηματική συσχέτιση των μοτίβων της τυρβώδους ροής των ρευστών, με τους στροβιλισμούς που απεικόνιζε στους πίνακές του ο Βαν Γκογκ. Σε άρθρο τους με τίτλο «Turbulent luminance in impassioned van Gogh paintings», έδειξαν ότι η συνάρτηση κατανομής της πιθανότητας των στροβιλισμών του φωτός σε ορισμένους πίνακες του μεταϊμπρεσιονιστή ζωγράφου, μοιάζει με την αντίστοιχη κατανομή των μεταβολών της ταχύτητας κατά την τυρβώδη ροή ρευστού, όπως προβλέπει η στατιστική θεωρία του Kolmogorov (που περιγράφει έστω και εν μέρει τη δυναμική των ρευστών). Τη δεκαετία του 1940, ο Σοβιετικός μαθηματικός Αντρέι Κολμογκόροφ περιέγραψε μια μαθηματική σχέση μεταξύ των διακυμάνσεων της ταχύτητας μιας ροής και του ρυθμού με τον οποίο διαχέεται η ενέργειά της, αναπτύσσοντας τη θεωρία της τύρβης του Kolmogorov. 

Το καλλιτεχνικό ενδιαφέρον εδώ είναι ότι η στατιστική υπογραφή της δυναμικής των ρευστών ανιχνεύεται μόνο στους πίνακες που συνέθεσε ο βαν Γκογκ στην ψυχολογικά διαταραγμένη περίοδο της ζωής του και όχι όταν η ζωή του κυλούσε ήρεμα.

Ο van Gogh και οι στροβιλισμοί του πάλι στο προσκήνιο

Φέτος, μια νέα ανάλυση του πίνακα από επιστήμονες από την Κίνα και τη Γαλλία «αποκαλύπτει» τα κρυμμένα μαθηματικά στην «Έναστρη Νύχτα».

«Φανταστείτε ότι στέκεστε σε μια γέφυρα και παρακολουθείτε το ποτάμι να κυλάει. Θα δείτε στροβιλισμούς στην επιφάνεια, και αυτοί οι στροβιλισμοί δεν είναι τυχαίοι. Εντάσσονται σε συγκεκριμένα μοτίβα και αυτά τα είδη μοτίβων μπορούν να προβλεφθούν από φυσικούς νόμους», δήλωσε ο Γιονγκ Τσιάνγκ Χουάνγκ,  επικεφαλής συγγραφέας της μελέτης η οποία δημοσιεύθηκε στο επιστημονικό περιοδικό Physics of Fluids. Ο Huang είναι ερευνητής στο State Key Laboratory of Marine Environmental Science & College of Ocean and Earth Sciences στο Πανεπιστήμιο Xiamen στη νοτιοανατολική Κίνα.

Με τη χρήση ενός ψηφιακού αντιγράφου του πίνακα, ο Χουάνγκ και οι συνάδελφοί του εξέτασαν την κλίμακα των 14 βασικών περιδινούμενων σχηματισμών για να κατανοήσουν αν συμμορφώνονταν με θεωρίες της φυσικής που περιγράφουν τη μεταφορά ενέργειας από μεγάλης σε μικρής κλίμακας περιδινήσεων καθώς συγκρούονται και αλληλεπιδρούν μεταξύ τους.

Ο ουρανός του πίνακα, καθώς είναι φιλοτεχνημένος και δεν κινείται πραγματικά, δεν μπορεί να μετρηθεί άμεσα, οπότε ο Χουάνγκ και οι συνάδελφοί του υπολόγισαν με ακρίβεια τις πινελιές, συγκρίνοντας το μέγεθός τους με μαθηματικές κλίμακες της τυρβώδους ροής.

Για να μετρήσουν τη φυσική κίνηση, χρησιμοποίησαν τη φωτεινότητα των διαφορετικών χρωμάτων που χρησιμοποίησε ο καλλιτέχνης.

Έτσι, ανακάλυψαν πως τα μεγέθη των 14 στροβίλων στην «Έναστρη Νύχτα» και η σχετική απόσταση και έντασή τους ακολουθούν τη θεωρία της τύρβης του Kolmogorov. 

Σύμφωνα με τον Χουάνγκ και την επιστημονική ομάδα του, ο πίνακας, σε μικρότερη κλίμακα, αναμειγνύεται με κάποιες δίνες και στροβιλισμούς υποβάθρου με τρόπο που προβλέπεται από τη θεωρία της τύρβης, ακολουθώντας ένα στατιστικό μοτίβο γνωστό ως κλίμακα του Batchelor (Batchelor’s scaling), που καθορίστηκε από τον George Batchelor και περιγράφει μαθηματικά τον τρόπο με τον οποίο τα μικρά σωματίδια, όπως τα παρασυρόμενα φύκια στον ωκεανό ή τα κομμάτια σκόνης στον άνεμο, αναμειγνύονται παθητικά από την τυρβώδη ροή. 

 

 

Άγνοια των μοντέλων – Μελέτη της φύσης

«Φυσικά», είπε ο Χουάνγκ, «ο βαν Γκογκ δεν θα γνώριζε τέτοιες θεωρίες ή εξισώσεις, αλλά πιθανότατα πέρασε πολύ χρόνο παρατηρώντας την τύρβη στη φύση… Νομίζω ότι αυτή η φυσική σχέση πρέπει να είναι ενσωματωμένη στο μυαλό του, γι’ αυτό όταν έκανε αυτόν τον διάσημο πίνακα "Έναστρη Νύχτα", μιμείται την πραγματική τυρβώδη ροή».

Φράση του καλλιτέχνη... Φωτογραφία αρχείου από την έκθεση "Van Gogh Alive" τον Μάρτιο του 2018 στην Αθήνα

Ο Χουάνγκ είπε ότι οι επιστήμονες προσπαθούν εδώ και πολύ καιρό να περιγράψουν την τυρβώδη ροή στη δυναμική των ρευστών με τρόπο που θα τους επιτρέπει να προβλέψουν το φαινόμενο. Μια διεξοδική κατανόηση της τυρβώδους ροής θα βοηθούσε στην πρόγνωση του καιρού, στις αναταράξεις των πτήσεων και σε πολλές άλλες διαδικασίες, ενώ μια πλήρης εξήγηση παραμένει ένα κυρίαρχο μυστήριο της φυσικής.

Πηγές - Παραπομπές

CNN: Turbulentskies of Vincent Van Gogh’s ‘The Starry Night’ align with a scientific theory,study finds

Phys.uoa.gr|Τύρβη

Physics4u

Physicsgg.me

ScienceDirect

TED-Ed|The unexpected math behind van Gogh's "Starry Night"

Turbulent Luminance in Impassioned van Gogh Paintings

University of Thessaly|Εισαγωγή σε Περιβαλλοντικές Ροές-Υπολογιστική Ρευστομηχανική και Τύρβη

Wikipedia.org

Περί του χρυσού αριθμού «φ»... (Μέρος 3º - Ο αγαπημένος αριθμός του σύμπαντος)

«Η Γεωμετρία έχει δύο μεγάλους θησαυρούς...

Ο ένας είναι το Πυθαγόρειο Θεώρημα,

ο άλλος η διαίρεση μιας γραμμής σε άκρο και μέσο λόγο.

Τον πρώτο μπορούμε να τον συγκρίνουμε με μια ποσότητα χρυσού.

Τον δεύτερο μπορούμε να τον θεωρήσουμε ως ένα πολύτιμο κόσμημα».

Johannes Kepler (1571 - 1630)

Όπως είχαμε δει στο 2º μέρος, ο χρυσός αριθμός φ = 1,618... δίνει το παρών σχεδόν παντού στη φύση, σε πολλούς ζωντανούς οργανισμούς, ακόμη και σε μοριακό επίπεδο. Συνεχίζοντας τώρα, ανακαλύπτουμε την παρουσία του φ όπου δεν μπορούσαμε να φανταστούμε... στο ίδιο μας το σώμα, στο DNA μας, ακόμη και στο Διάστημα!

Ο ΑΡΙΘΜΟΣ φ ΣΤΟ ΑΝΘΡΩΠΙΝΟ ΣΩΜΑ

Στοv «άνθρωπο του Βιτρούβιου», το διάσημο σχέδιο του Da Vinci, βλέπουμε, μετά από μια "σύγχρονη" παρέμβαση, τις χρυσές αναλογίες στο ανθρώπινο σώμα. Ήταν ο ίδιος ο Da Vinci που ονόμασε τον φ «χρυσό αριθμό», ενώ ο συνεργάτης του, μαθηματικός και μοναχός, Luca Pacioli, έγραψε το βιβλίο «Περί της Θείας Αναλογίας», αναφερόμενος στο λόγο της χρυσής τομής. Το θέμα του βιβλίου είναι η αναλογία στα μαθηματικά και την τέχνη, ιδίως η θεωρία της χρυσής τομής και η εφαρμογή της στην αρχιτεκτονική.

O αριθμός φ εμφανίζεται σε πολλές από τις αναλογίες του ανθρώπινου σώματος. Για παράδειγμα, ο αφαλός «τέμνει» το σώμα μας, από την κορυφή του κεφαλιού μέχρι τα δάκτυλα των ποδιών, σε λόγο χρυσής τομής. Αν μετρήσετε το ύψος σας (την απόσταση από την κορυφή του κεφαλιού σας μέχρι το πάτωμα) και τη διαιρέσετε με την απόσταση από τον αφαλό μέχρι το πάτωμα, προσεγγίζεται πάντα ο αριθμός φ. Αν μετρήσετε την απόσταση από τον αφαλό μέχρι το πάτωμα και τη διαιρέσετε με την απόσταση από την κορυφή του κεφαλιού σας μέχρι τον αφαλό, προσεγγίζεται πάντα ο αριθμός φ.  

Ακόμα, το χέρι μας, από τον ώμο μέχρι τις άκρες των δακτύλων μας, διαιρείται σε λόγο χρυσής τομής ακριβώς στον αγκώνα μας. Αν μετρήσετε την απόσταση από τον ώμο σας μέχρι τις άκρες των δακτύλων και τη διαιρέσετε με την απόσταση από τον αγκώνα μέχρι τις άκρες των δακτύλων, προσεγγίζεται  πάντα ο αριθμός φ. Αν μετρήσετε την απόσταση από τον αγκώνα μέχρι τις άκρες των δακτύλων και τη διαιρέσετε με την απόσταση από τον ώμο σας μέχρι τον αγκώνα, προσεγγίζεται  πάντα ο αριθμός φ.

Αντίστοιχα, ο καρπός «τέμνει» το χέρι μας, από τον αγκώνα μέχρι τις άκρες των δακτύλων, σε χρυσή τομή.

Όμοια, η χρυσή τομή και η ακολουθία Fibonacci μπορούν να βρεθούν και στα δάκτυλά μας. 

Η αναλογία μεταξύ του μήκους και του φάρδους του προσώπου και η αναλογία του μήκους του στόματος προς το φάρδος της μύτης είναι μερικά ακόμα παραδείγματα της εφαρμογής των αριθμών αυτών στο ανθρώπινο σώμα.

Ακόμα και σε πολλές άλλες λεπτομέρειες συναντάμε τον αριθμό φ, όπως στις αναλογίες των δοντιών μας ή του αυτιού μας. Φυσικά, δεν έχουμε όλοι ίδια δόντια, ίδια μύτη ή ίδια αυτιά. Απλώς, όσο περισσότερο πλησιάζουν οι αναλογίες κάποιου χαρακτηριστικού στον αριθμό φ, τόσο πιο «όμορφο» φαίνεται αυτό. 

Δεν είναι τυχαίο ότι πολλές «ανατολίτικες θρησκείες» και κινήματα στα πλαίσια της διδασκαλίας τους για διαλογισμό και την αυτοσυγκέντρωση και στο λεγόμενο «γιόγκα» η στάση του ανθρώπινου σώματος γίνεται κατά αυτό τον τρόπο έτσι, ώστε τα «κεντρικά - κομβικά» σημεία του σώματος να βρίσκονται σε αναλογίες φ.

Επιπλέον, έχει ανακαλυφθεί η ύπαρξη του φ στην δομή του DNA. Το DNA αποτελείται από δύο έλικες οι οποίες συστρέφονται μεταξύ τους. Οι αποστάσεις μεταξύ τους (grooves) «κρύβουν» τον αριθμό φ, όπως βλέπουμε παρακάτω:

Ο ΑΡΙΘΜΟΣ φ ΣΤΗΝ ΙΑΤΡΙΚΗ

Ένα καρδιογράφημα σε κατάσταση ηρεμίας μοιάζει με το παρακάτω. Θεωρείται υγιές όταν το διάστημα μεταξύ δύο οξέων επαρμάτων QRS διαιρείται σε λόγο χρυσής τομής από ένα έπαρμα Τ (το κόκκινο βέλος στο διάγραμμα).

Ο ΑΡΙΘΜΟΣ φ ΣΤΗ ΜΕΤΕΩΡΟΛΟΓΙΑ

Ο αριθμός φ και η χρυσή έλικα εμφανίζονται επίσης στο σχήμα των κυκλώνων, όπως αποτυπώνεται χαρακτηριστικά στις φωτογραφίες των μετεωρολογικών δορυφόρων.

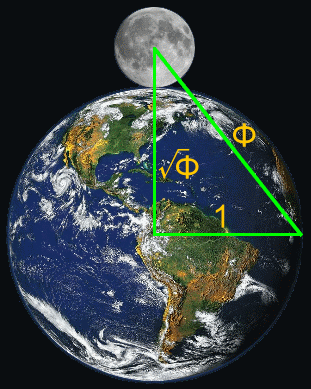
Ο ΑΡΙΘΜΟΣ φ ΣΤΟ ΗΛΙΑΚΟ ΜΑΣ ΣΥΣΤΗΜΑ

Οι διαστάσεις της Γης και της Σελήνης σχετίζονται με τον αριθμό φ, σχηματίζοντας ένα ορθογώνιο τρίγωνο βασισμένο στη χρυσή αναλογία.

H κίνηση ορισμένων πλανητών γίνεται βάσει του αριθμού φ, καθώς ο χρόνος περιφοράς τους γύρω από τον Ήλιο προσεγγίζεται από κάποια δύναμη του φ.

• Ερμής: φ^-3 = 0,24 έτη 
• Αφροδίτη: φ^-1 = 0,62 έτη
• Γη: φ⁰ = 1 έτος
• Δίας: φ⁵ = 11,9 έτη 
• Κρόνος: φ⁷ = 29 έτη

Ειδικότερα, ο Κρόνος έχει «αποκαλύψει» την αναλογία της χρυσής τομής στις διαστάσεις αυτού και των δακτυλίων του.

ΓΑΛΑΞΙΕΣ ΚΑΙ ΜΑΥΡΕΣ ΤΡΥΠΕΣ

Τα περισσότερα αντικείμενα θερμαίνονται καθώς προσλαμβάνουν ενέργεια. Αλλά ενίοτε οι μαύρες τρύπες ενδέχεται να χάνουν ενέργεια ενώ θερμαίνονται. Σ’ αυτή την περίπτωση, λέμε ότι έχουν αρνητική ειδική θερμοχωρητικότητα. 

Για μια περιστρεφόμενη μαύρη τρύπα, τα πράγματα περιπλέκονται περισσότερο. Όταν περιστρέφεται αρκετά γρήγορα, η ειδική θερμοχωρητικότητά της γίνεται θετική, όπως δηλαδή συμβαίνει με ένα συνηθισμένο αντικείμενο. Τη χρονική στιγμή που η ειδική θερμοχωρητικότητα της μαύρης τρύπας γίνεται από αρνητική θετική, η στροφορμή της J και η μάζα της M ικανοποιούν τη σχέση:

Συμμετέχει, δηλαδή, στην εξίσωση και ο αριθμός φ!

Τέλος, ο αριθμός φ και η χρυσή έλικα εμφανίζονται και στη μορφή των σπειροειδών γαλαξιών.

ΤΟ ΚΑΛΥΤΕΡΟ ΣΥΣΤΗΜΑ ΟΡΓΑΝΩΣΗΣ

Ποιος είναι άραγε ο βαθύτερος λόγος που κάνει έναν αριθμό, κατασκευασμένο με βάση μια αφηρημένη μαθηματική ιδιότητα, να έχει τόσο σημαντικές εφαρμογές στη φύση, και μάλιστα σε τόσο διαφορετικά συστήματα; Οι σπόροι, τα όστρακα, οι κυκλώνες και οι γαλαξίες δεν έχουν καμία κοινή ιδιότητα και διέπονται από εντελώς διαφορετικούς φυσικούς νόμους. (Βάρβογλης, 2003).  Όμως όλα τους εμπεριέχουν το χρυσό αριθμό.

Τα φύλλα, τα πέταλα και οι σπόροι οργανώνονται στα φυτά ακολουθώντας ένα συγκεκριμένο μοτίβο γιατί έτσι, καθώς αναπτύσσονται, αξιοποιούν με τον καλύτερο δυνατό τρόπο το διαθέσιμο χώρο. Αν κατανείμουμε τα φύλλα στο μίσχο σύμφωνα με το χρυσό αριθμό, όλα θα επωφελούνται στο μέγιστο βαθμό από το φως του ήλιου, χωρίς να κρύβει το ένα το άλλο. Τα λουλούδια, χάρη στο χρυσό αριθμό, προσελκύουν όσο το δυνατόν καλύτερα τα έντομα που μεταφέρουν τη γύρη.

Η ανάπτυξη των οστράκων επηρεάζεται από τον διαθέσιμο χώρο. Η δημιουργία των κυκλώνων οφείλεται στη ροή του υγρού αέρα από περιοχές υψηλής πίεσης σε περιοχές χαμηλής. 

Λόγω της περιστροφής της Γης, τα ρεύματα του αέρα αποκλίνουν από την ευθεία, έτσι ώστε στο βόρειο ημισφαίριο όλοι οι κυκλώνες να περιστρέφονται αντίθετα από τη φορά των δεικτών του ρολογιού, ενώ στο νότιο ημισφαίριο, αντίστροφα. 

Τέλος οι σπείρες είναι περιοχές ενός γαλαξία όπου υπάρχει συγκέντρωση αστέρων, σκόνης και αερίων, οι οποίες δημιουργούνται όταν κάποιος άλλος γαλαξίας περάσει σε κοντινή απόσταση. 

Φαίνεται, λοιπόν, ότι ο χρυσός αριθμός έχει «παγκόσμιες» ιδιότητες και είναι ο αγαπημένος αριθμός του Σύμπαντος. Κι αν έχει επιλέξει η Φύση να «δουλεύει» χρησιμοποιώντας τη χρυσή αναλογία, τότε γιατί όχι και ο άνθρωπος;

Στα επόμενα θα δούμε πώς οι άνθρωποι εφαρμόζουν τη Χρυσή Τομή από την αρχαιότητα μέχρι σήμερα…

Πηγές:

Περιοδικό Focus

goldennumber.net

wikipedia.org

https://johncarlosbaez.wordpress.com/2013/02/28/black-holes-and-the-golden-ratio/