"Αριθμητική με το νου"

Ο Nikolay Bogdanov-Belsky (1868 - 1945) ήταν Ρώσος ζωγράφος που ακολουθούσε τα ρεύματα του Ρεαλισμού και του Ιμπρεσιονισμού. Πολλά από τα έργα του έχουν ηθογραφικό χαρακτήρα και αποτελούνται από πορτρέτα, ιμπρεσιονιστικά τοπία και απεικονίσεις της καθημερινής ζωής, με κύριο στοιχείο τα παιδιά και την εκπαίδευση τους.

To 1895, o Nikolay Bogdanov-Belsky ζωγράφισε τον πίνακα «Αριθμητική με το νου. Στο δημόσιο σχολείο του S. Rachinsky», ή κατ' άλλους, «Ένα δυσνόητο πρόβλημα». Ο δάσκαλος που απεικονίζεται είναι ο S. Rachinsky, καθηγητής φυσικής, ο οποίος εγκατέλειψε το πανεπιστήμιο για να υπηρετήσει ως απλός δάσκαλος σε κάποιο χωριό.

Οι περισσότεροι, όμως, όταν θαυμάζουν το έργο τέχνης, παραβλέπουν το πρόβλημα που είναι γραμμένο στον πίνακα της τάξης... Το πρόβλημα ζητάει τον υπολογισμό της αριθμητικής παράστασης:

(10²+11²+12²+13²+14²)/365

Μπορείτε να κάνετε τον υπολογισμό με το μυαλό σας;

Πηγές:

Yakov Perelman, Διασκεδαστικά Μαθηματικά, Εκδόσεις Κάτοπτρο, 2001

https://twitter.com/fermatslibrary

Περί του χρυσού αριθμού «φ»... (Μέρος 3º - Ο αγαπημένος αριθμός του σύμπαντος)

«Η Γεωμετρία έχει δύο μεγάλους θησαυρούς...

Ο ένας είναι το Πυθαγόρειο Θεώρημα,

ο άλλος η διαίρεση μιας γραμμής σε άκρο και μέσο λόγο.

Τον πρώτο μπορούμε να τον συγκρίνουμε με μια ποσότητα χρυσού.

Τον δεύτερο μπορούμε να τον θεωρήσουμε ως ένα πολύτιμο κόσμημα».

Johannes Kepler (1571 - 1630)

Όπως είχαμε δει στο 2º μέρος, ο χρυσός αριθμός φ = 1,618... δίνει το παρών σχεδόν παντού στη φύση, σε πολλούς ζωντανούς οργανισμούς, ακόμη και σε μοριακό επίπεδο. Συνεχίζοντας τώρα, ανακαλύπτουμε την παρουσία του φ όπου δεν μπορούσαμε να φανταστούμε... στο ίδιο μας το σώμα, στο DNA μας, ακόμη και στο Διάστημα!

Ο ΑΡΙΘΜΟΣ φ ΣΤΟ ΑΝΘΡΩΠΙΝΟ ΣΩΜΑ

Στοv «άνθρωπο του Βιτρούβιου», το διάσημο σχέδιο του Da Vinci, βλέπουμε, μετά από μια "σύγχρονη" παρέμβαση, τις χρυσές αναλογίες στο ανθρώπινο σώμα. Ήταν ο ίδιος ο Da Vinci που ονόμασε τον φ «χρυσό αριθμό», ενώ ο συνεργάτης του, μαθηματικός και μοναχός, Luca Pacioli, έγραψε το βιβλίο «Περί της Θείας Αναλογίας», αναφερόμενος στο λόγο της χρυσής τομής. Το θέμα του βιβλίου είναι η αναλογία στα μαθηματικά και την τέχνη, ιδίως η θεωρία της χρυσής τομής και η εφαρμογή της στην αρχιτεκτονική.

O αριθμός φ εμφανίζεται σε πολλές από τις αναλογίες του ανθρώπινου σώματος. Για παράδειγμα, ο αφαλός «τέμνει» το σώμα μας, από την κορυφή του κεφαλιού μέχρι τα δάκτυλα των ποδιών, σε λόγο χρυσής τομής. Αν μετρήσετε το ύψος σας (την απόσταση από την κορυφή του κεφαλιού σας μέχρι το πάτωμα) και τη διαιρέσετε με την απόσταση από τον αφαλό μέχρι το πάτωμα, προσεγγίζεται πάντα ο αριθμός φ. Αν μετρήσετε την απόσταση από τον αφαλό μέχρι το πάτωμα και τη διαιρέσετε με την απόσταση από την κορυφή του κεφαλιού σας μέχρι τον αφαλό, προσεγγίζεται πάντα ο αριθμός φ.  

Ακόμα, το χέρι μας, από τον ώμο μέχρι τις άκρες των δακτύλων μας, διαιρείται σε λόγο χρυσής τομής ακριβώς στον αγκώνα μας. Αν μετρήσετε την απόσταση από τον ώμο σας μέχρι τις άκρες των δακτύλων και τη διαιρέσετε με την απόσταση από τον αγκώνα μέχρι τις άκρες των δακτύλων, προσεγγίζεται  πάντα ο αριθμός φ. Αν μετρήσετε την απόσταση από τον αγκώνα μέχρι τις άκρες των δακτύλων και τη διαιρέσετε με την απόσταση από τον ώμο σας μέχρι τον αγκώνα, προσεγγίζεται  πάντα ο αριθμός φ.

Αντίστοιχα, ο καρπός «τέμνει» το χέρι μας, από τον αγκώνα μέχρι τις άκρες των δακτύλων, σε χρυσή τομή.

Όμοια, η χρυσή τομή και η ακολουθία Fibonacci μπορούν να βρεθούν και στα δάκτυλά μας. 

Η αναλογία μεταξύ του μήκους και του φάρδους του προσώπου και η αναλογία του μήκους του στόματος προς το φάρδος της μύτης είναι μερικά ακόμα παραδείγματα της εφαρμογής των αριθμών αυτών στο ανθρώπινο σώμα.

Ακόμα και σε πολλές άλλες λεπτομέρειες συναντάμε τον αριθμό φ, όπως στις αναλογίες των δοντιών μας ή του αυτιού μας. Φυσικά, δεν έχουμε όλοι ίδια δόντια, ίδια μύτη ή ίδια αυτιά. Απλώς, όσο περισσότερο πλησιάζουν οι αναλογίες κάποιου χαρακτηριστικού στον αριθμό φ, τόσο πιο «όμορφο» φαίνεται αυτό. 

Δεν είναι τυχαίο ότι πολλές «ανατολίτικες θρησκείες» και κινήματα στα πλαίσια της διδασκαλίας τους για διαλογισμό και την αυτοσυγκέντρωση και στο λεγόμενο «γιόγκα» η στάση του ανθρώπινου σώματος γίνεται κατά αυτό τον τρόπο έτσι, ώστε τα «κεντρικά - κομβικά» σημεία του σώματος να βρίσκονται σε αναλογίες φ.

Επιπλέον, έχει ανακαλυφθεί η ύπαρξη του φ στην δομή του DNA. Το DNA αποτελείται από δύο έλικες οι οποίες συστρέφονται μεταξύ τους. Οι αποστάσεις μεταξύ τους (grooves) «κρύβουν» τον αριθμό φ, όπως βλέπουμε παρακάτω:

Ο ΑΡΙΘΜΟΣ φ ΣΤΗΝ ΙΑΤΡΙΚΗ

Ένα καρδιογράφημα σε κατάσταση ηρεμίας μοιάζει με το παρακάτω. Θεωρείται υγιές όταν το διάστημα μεταξύ δύο οξέων επαρμάτων QRS διαιρείται σε λόγο χρυσής τομής από ένα έπαρμα Τ (το κόκκινο βέλος στο διάγραμμα).

Ο ΑΡΙΘΜΟΣ φ ΣΤΗ ΜΕΤΕΩΡΟΛΟΓΙΑ

Ο αριθμός φ και η χρυσή έλικα εμφανίζονται επίσης στο σχήμα των κυκλώνων, όπως αποτυπώνεται χαρακτηριστικά στις φωτογραφίες των μετεωρολογικών δορυφόρων.

Ο ΑΡΙΘΜΟΣ φ ΣΤΟ ΗΛΙΑΚΟ ΜΑΣ ΣΥΣΤΗΜΑ

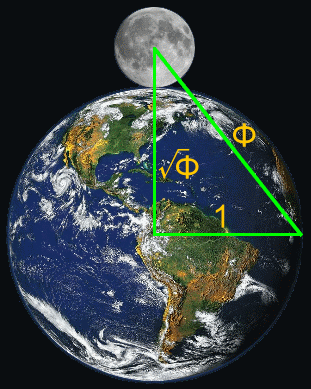
Οι διαστάσεις της Γης και της Σελήνης σχετίζονται με τον αριθμό φ, σχηματίζοντας ένα ορθογώνιο τρίγωνο βασισμένο στη χρυσή αναλογία.

H κίνηση ορισμένων πλανητών γίνεται βάσει του αριθμού φ, καθώς ο χρόνος περιφοράς τους γύρω από τον Ήλιο προσεγγίζεται από κάποια δύναμη του φ.

• Ερμής: φ^-3 = 0,24 έτη 
• Αφροδίτη: φ^-1 = 0,62 έτη
• Γη: φ⁰ = 1 έτος
• Δίας: φ⁵ = 11,9 έτη 
• Κρόνος: φ⁷ = 29 έτη

Ειδικότερα, ο Κρόνος έχει «αποκαλύψει» την αναλογία της χρυσής τομής στις διαστάσεις αυτού και των δακτυλίων του.

ΓΑΛΑΞΙΕΣ ΚΑΙ ΜΑΥΡΕΣ ΤΡΥΠΕΣ

Τα περισσότερα αντικείμενα θερμαίνονται καθώς προσλαμβάνουν ενέργεια. Αλλά ενίοτε οι μαύρες τρύπες ενδέχεται να χάνουν ενέργεια ενώ θερμαίνονται. Σ’ αυτή την περίπτωση, λέμε ότι έχουν αρνητική ειδική θερμοχωρητικότητα. 

Για μια περιστρεφόμενη μαύρη τρύπα, τα πράγματα περιπλέκονται περισσότερο. Όταν περιστρέφεται αρκετά γρήγορα, η ειδική θερμοχωρητικότητά της γίνεται θετική, όπως δηλαδή συμβαίνει με ένα συνηθισμένο αντικείμενο. Τη χρονική στιγμή που η ειδική θερμοχωρητικότητα της μαύρης τρύπας γίνεται από αρνητική θετική, η στροφορμή της J και η μάζα της M ικανοποιούν τη σχέση:

Συμμετέχει, δηλαδή, στην εξίσωση και ο αριθμός φ!

Τέλος, ο αριθμός φ και η χρυσή έλικα εμφανίζονται και στη μορφή των σπειροειδών γαλαξιών.

ΤΟ ΚΑΛΥΤΕΡΟ ΣΥΣΤΗΜΑ ΟΡΓΑΝΩΣΗΣ

Ποιος είναι άραγε ο βαθύτερος λόγος που κάνει έναν αριθμό, κατασκευασμένο με βάση μια αφηρημένη μαθηματική ιδιότητα, να έχει τόσο σημαντικές εφαρμογές στη φύση, και μάλιστα σε τόσο διαφορετικά συστήματα; Οι σπόροι, τα όστρακα, οι κυκλώνες και οι γαλαξίες δεν έχουν καμία κοινή ιδιότητα και διέπονται από εντελώς διαφορετικούς φυσικούς νόμους. (Βάρβογλης, 2003).  Όμως όλα τους εμπεριέχουν το χρυσό αριθμό.

Τα φύλλα, τα πέταλα και οι σπόροι οργανώνονται στα φυτά ακολουθώντας ένα συγκεκριμένο μοτίβο γιατί έτσι, καθώς αναπτύσσονται, αξιοποιούν με τον καλύτερο δυνατό τρόπο το διαθέσιμο χώρο. Αν κατανείμουμε τα φύλλα στο μίσχο σύμφωνα με το χρυσό αριθμό, όλα θα επωφελούνται στο μέγιστο βαθμό από το φως του ήλιου, χωρίς να κρύβει το ένα το άλλο. Τα λουλούδια, χάρη στο χρυσό αριθμό, προσελκύουν όσο το δυνατόν καλύτερα τα έντομα που μεταφέρουν τη γύρη.

Η ανάπτυξη των οστράκων επηρεάζεται από τον διαθέσιμο χώρο. Η δημιουργία των κυκλώνων οφείλεται στη ροή του υγρού αέρα από περιοχές υψηλής πίεσης σε περιοχές χαμηλής. 

Λόγω της περιστροφής της Γης, τα ρεύματα του αέρα αποκλίνουν από την ευθεία, έτσι ώστε στο βόρειο ημισφαίριο όλοι οι κυκλώνες να περιστρέφονται αντίθετα από τη φορά των δεικτών του ρολογιού, ενώ στο νότιο ημισφαίριο, αντίστροφα. 

Τέλος οι σπείρες είναι περιοχές ενός γαλαξία όπου υπάρχει συγκέντρωση αστέρων, σκόνης και αερίων, οι οποίες δημιουργούνται όταν κάποιος άλλος γαλαξίας περάσει σε κοντινή απόσταση. 

Φαίνεται, λοιπόν, ότι ο χρυσός αριθμός έχει «παγκόσμιες» ιδιότητες και είναι ο αγαπημένος αριθμός του Σύμπαντος. Κι αν έχει επιλέξει η Φύση να «δουλεύει» χρησιμοποιώντας τη χρυσή αναλογία, τότε γιατί όχι και ο άνθρωπος;

Στα επόμενα θα δούμε πώς οι άνθρωποι εφαρμόζουν τη Χρυσή Τομή από την αρχαιότητα μέχρι σήμερα…

Πηγές:

Περιοδικό Focus

goldennumber.net

wikipedia.org

https://johncarlosbaez.wordpress.com/2013/02/28/black-holes-and-the-golden-ratio/

Διανυσματικός Λογισμός στο "Star Wars"

Πριν από πολύ καιρό, σε μια τάξη πολύ - πολύ μακριά...

Γρίφος: Άλματα στο χρόνο

"Ξέρεις κάτι;" μου είπε ένας φίλος μου. "Προχθές ήμουν 10 ετών και του χρόνου θα γίνω 13!"

Είναι δυνατόν να έλεγε την αλήθεια;;;

Πηγη:
ΜΑΘΗΜΑΤΙΚΟΙ ΓΡΙΦΟΙ 2 - 150 προβλήματα από τη στήλη "Σπαζοκεφαλιές" του περιοδικού Quantum, εκδόσεις "Κάτοπτρο"

Γραμμικό σύστημα 2x2 και η απάντηση ενός μαθητή...

Βρες το ζεύγος των αριθμών x και y που επαληθεύει το παραπάνω σύστημα.

Μαθηματικά και παιχνίδι: Τα σπιτάκια των αριθμών

Καλή σχολική χρονιά σε μικρούς και μεγάλους και επισήμως!

Για τους δασκάλους στο Δημοτικό, αλλά και για τους γονείς που έχουν μικρά παιδιά, αποφάσισα να εγκαινιάσω σ' αυτό το ιστολόγιο μια νέα κατηγορία με θέμα "Μαθηματικά και Παιχνίδι". Ως εκπαιδευτικός και γονέας η ίδια, καταλαβαίνω κάθε δυσκολία που μπορεί να αντιμετωπίζουν τα μικρά παιδιά όσον αφορά τα Μαθηματικά. Σύμφωνα με ακαδημαϊκές έρευνες, όταν ένας γονέας δείχνει ενδιαφέρον και μεράκι (και όχι φόβο-απέχθεια) για τα Μαθηματικά, το παιδί δεν θα δυσκολευτεί να τα κατανοήσει και ίσως αποκτήσει το ίδιο ενδιαφέρον και αυτό. 

Είναι πολύ σημαντικό για τα παιδιά να πάρουν τα Μαθηματικά "με καλό μάτι" από την αρχή και σ' αυτό μπορείτε να τα βοηθήσετε παίζοντας μαζί τους παιχνίδια με αριθμούς. Όταν η κόρη μου ήταν στο στάδιο της πρόσθεσης με τα δάχτυλα (αρχές Α΄ Δημοτικού), είχαμε κάνει μαζί μια διασκεδαστική χειροτεχνία που βοήθησε την μικρή μου μαθήτρια να εμπεδώσει τα αθροίσματα που δεν ξεπερνούν το 10. Ήταν τα "σπιτάκια των αριθμών"...

"Τα σπιτάκια των αριθμών"

Κάθε σπιτάκι είχε στη στέγη του έναν αριθμό από το 1 ως το 10. Έτσι, τα ονομάσαμε ως "το σπιτάκι του 1", "το σπιτάκι του 2", κ.ο.κ. Έπειτα κολλήσαμε μαζί, πάνω σε κάθε σπιτάκι, όλα τα αθροίσματα που έδιναν τον αριθμό της σκεπής. 

    

  

   

Κάθε φορά που κολλούσαμε ένα άθροισμα, λέγαμε φωναχτά την προσθεσούλα για να την εμπεδώσουμε.

Ειδικά, το "σπιτάκι του 10" που περιέχει τα αθροίσματα στο 10 είναι πολύ σημαντικό να το μάθουν τα πιτσιρίκια. Θα μας βοηθήσει αργότερα στην πρόσθεση μεγαλύτερων αριθμών που γίνεται με το "πάτημα στη δεκάδα". Π.χ. για το 8+6, θα "πατήσουμε" στο 10 και θα πούμε: (8+2)+4=10+4=14.

Είναι, λοιπόν, κατά τη γνώμη μου, ένας πολύ διασκεδαστικός τρόπος για τα παιδιά να εμπεδώσουν την πρόσθεση και, σαν χειροτεχνία δεν είναι δύσκολη!

Μπορείτε να την εφαρμόσετε κι εσείς με τα παιδιά σας ή τους μαθητές σας! Η δραστηριότητα αυτή είναι κατάλληλη ακόμη και στην περίπτωση που κάποιο παιδί αντιμετωπίζει ειδικές μαθησιακές δυσκολίες.

• Για την προετοιμασία έχετε να γράψετε σε αρχείο word όλα τα αθροίσματα που δεν ξεπερνούν το 10, καθώς και τους αριθμούς από το 1 ως το 10 σε κάπως μεγαλύτερη γραμματοσειρά. Εναλλακτικά, ζητήστε μου να σας στείλω το δικό μου αρχείο με e-mail! 

• Τυπώστε τους αριθμούς σε απλό ή χρωματιστό χαρτί εκτύπωσης.

Για τη χειροτεχνία θα χρειστείτε:

-Χαρτόνια κάνσον

-Μολύβι

-Χάρακα

-Ψαλίδι

-Κόλλα στικ

Σχεδιάζετε στα χαρτόνια και κόβετε 10 ορθογώνια και 10 τρίγωνα σχήματα για τα σπιτάκια. Κόβετε και τους αριθμούς και τα αθροίσματα που έχετε εκτυπώσει. Έπειτα τα κολλάτε στα σπιτάκια παίζοντας και επαναλαμβάνοντας τις προσθεσούλες! 

Να πω καλό διάβασμα? Θα πω καλό παιχνίδι!!!

  

~*~*~*~*~

Σημείωση: Η παραπάνω ανάρτηση αποτελεί αναδημοσίευση από το παλιό μου ιστολόγιο. Μπορείτε να διαβάσετε την πρωτότυπη ανάρτηση εδώ...

~*~*~*~*~

"Αν οι αριθμοί δεν είναι όμορφοι, δεν ξέρω τι είναι όμορφο".

Paul Erdos (1913 - 1996)

"Kill the Puzzle"

Καλό μήνα σε όλους! Παρακάτω σας έχω μια μαθηματική πρόκληση που βρήκα στο διαδίκτυο... Σας προειδοποιώ πως δεν είναι όσο εύκολη φαίνεται με την πρώτη ματιά, αλλά θέλει προσοχή και παρατηρητικότητα. Θα δοκιμάσετε;;;

KILL THE PUZZLE!!!

Τα Μαθηματικά στην Τέχνη: Συμμετρία

Η ισορροπία είναι μια αρχή της σχεδίασης που βασίζεται στο οπτικό βάρος των αντικειμένων. Τα έργα τέχνης γίνονται πιο ελκυστικά όταν τα μέρη τους ισορροπούν και ένας τρόπος για να το πετύχει αυτό ο καλλιτέχνης είναι η συμμετρία. Τι είναι ακριβώς η συμμετρία;

ΣΥΜΜΕΤΡΙΑ ΩΣ ΠΡΟΣ ΑΞΟΝΑ

Τα βιβλία γράφουν...

Έστω ότι έχουμε ένα σημείο Α, σημειωμένο σε ένα φύλλο χαρτί. Συμμετρικό σημείου Α ως προς ευθεία ε, είναι το σημείο Α΄, το οποίο, αν διπλώσουμε το φύλλο κατά μήκος της ευθείας ε, θα συμπίπτει με το Α.

Δύο σχήματα λέγονται συμμετρικά ως προς μια ευθεία ε, όταν καθένα αποτελείται από τα συμμετρικά σημεία του άλλου ως προς την ευθεία ε.

Τα συμμετρικά ως προς ευθεία σχήματα είναι ίσα.

Kazuya Akimoto (Σύγχρονος ζωγράφος) - "Black Bat" (2009)

Kazuya Akimoto (Σύγχρονος ζωγράφος) - "Autumn Night" (2008)

Roland Rafael Repczuk (Σύγχρονος ζωγράφος) - "Knowledge" (2001)

Leigh Ann Inskeep-Simpson (Σύγχρονη ζωγράφος και καθηγήτρια καλλιτεχνικών) - "Symmetrical Garden" (2011)

Leigh Ann Inskeep-Simpson (Σύγχρονη ζωγράφος και καθηγήτρια καλλιτεχνικών) - "Looking Out My Back Door" (2011)

Τα βιβλία γράφουν...

Άξονας συμμετρίας σχήματος ονομάζεται η ευθεία που χωρίζει το σχήμα σε δύο μέρη, τα οποία συμπίπτουν όταν διπλωθεί το σχήμα κατά μήκος της ευθείας. Στην περίπτωση αυτή, λέμε ότι το σχήμα έχει άξονα συμμετρίας την ευθεία αυτή.

Όταν ένα σχήμα έχει άξονα συμμετρίας, το συμμετρικό του ως προς τον άξονα συμμετρίας είναι το ίδιο το σχήμα.

Μαρία Λιναρδάτου (Σύγχρονη ζωγράφος - ιστορικός τέχνης - καθηγήτρια καλλιτεχνικών)
Διδασκαλία της συμμετρίας μέσα από την τέχνη με πεταλούδες

Μαρία Λιναρδάτου (Σύγχρονη ζωγράφος - ιστορικός τέχνης - καθηγήτρια καλλιτεχνικών)
Διδασκαλία δημιουργίας συμμετρικού σχήματος

ΣΥΜΜΕΤΡΙΑ ΩΣ ΠΡΟΣ ΣΗΜΕΙΟ

Τα βιβλία γράφουν...

Συμμετρικό σημείου Α ως προς κέντρο Ο, είναι το σημείο Α΄, με το οποίο συμπίπτει το Α, αν περιστραφεί γύρω από το Ο κατά 180º.

Δύο σχήματα λέγονται συμμετρικά ως προς σημείο Ο, όταν κάθε σημείο του ενός είναι συμμετρικό ενός σημείου του άλλου
ως προς το Ο.
Τα συμμετρικά ως προς σημείο σχήματα είναι ίσα.

Brian Sloan (Σύγχρονος ζωγράφος) - "Roses in Symmetry"

Dona Morgan Greer (Σύγχρονη ζωγράφος) - "Harmony" (2015)

Τα βιβλία γράφουν...

Κέντρο συμμετρίας σχήματος ονομάζεται ένα σημείο του Ο, γύρω από το οποίο αν περιστραφεί το σχήμα κατά 180º, συμπίπτει με το αρχικό. Στην περίπτωση που υπάρχει τέτοιο σημείο, λέμε ότι το σχήμα έχει κέντρο συμμετρίας το Ο.

Όταν ένα σχήμα έχει κέντρο συμμετρίας, το συμμετρικό του ως προς το κέντρο συμμετρίας είναι το ίδιο το σχήμα.

Kazuya Akimoto (Σύγχρονος ζωγράφος) - "Golden Baby Twins" (2010)

Πηγές:

• Μαθηματικά Α' Γυμνασίου, Ινστιτούτο Τεχνολογίας Υπολογιστών και Εκδόσεων "Διόφαντος", 2016
• E.H. Gombrich, Το Χρονικό της Τέχνης, Μορφωτικό Ίδρυμα Εθνικής Τραπέζης, 1995
• Wassily Kandinsky, Σημείο-Γραμμή-Επίπεδο, Εκδόσεις Δωδώνη, 2013
• H.L.C Jaffe, Η ζωγραφική στον 20ό αιώνα, Εκδόσεις Νεφέλη, 1984
• Brian Sloan Paintings
• Dona Morgan
• Kazuya Akimoto
• Leigh Ann Inskeep-Simpson
• Maria Linardatou
• Roland Raphael Repczuk: Symmetrical Surrealism
• wikipedia.org

Τα Μαθηματικά στην Τέχνη: Οι ευθείες στο επίπεδο

Συχνά οι καλλιτέχνες χρησιμοποιούν στα έργα τους σχέδια, σημεία, ευθείες και άλλα αντικείμενα. Ο συλλογισμός τους μπορεί να επιτρέψει την απάντηση στα εξής ερωτήματα: Τι είναι ένα σημείο; Τι είναι ευθεία; Τι εννοούμε με τον όρο "παραλληλία"; Ο Wassily Kandinsky (1866 - 1944) ήταν Ρώσος ζωγράφος, ποιητής, δραματουργός και παιδαγωγός, ενώ είχε επίσης σπουδάσει νομική και οικονομικά. Τις πανεπιστημιακές του γνώσεις τις είχε εντάξει στο σχέδιο και στη ζωγραφική του. Από την εμπειρία του ως καθηγητής, άντλησε το υλικό της πραγματείας του "Σημείο - Γραμμή - Επίπεδο" (1925). Ο Kandinsky ορίζει τη γραμμή ως "ένα μοναδικό σημείο που σύρεται πάνω σε μια σελίδα".

Στο πλαίσιο του project "Μαθηματικά και Τέχνη", μαθαίνουμε σήμερα, μέσα από την τέχνη, για τις ευθείες στο επίπεδο...

ΕΥΘΕΙΕΣ ΣΤΟ ΕΠΙΠΕΔΟ

Τα βιβλία γράφουν...

Δύο διαφορετικές ευθείες που βρίσκονται στο ίδιο επίπεδο ή θα είναι παράλληλες, ή θα τέμνονται.

ΠΑΡΑΛΛΗΛΕΣ ΕΥΘΕΙΕΣ

Kazimir Malevich (1878 - 1935) - "Red Cavalry Parallels"

James Charles (σύγχρονος ζωγράφος) - "Straight Lines"

Ellsworth Kelly (1923 - 2015) - "Spectrum IV" (1967)

Joanne Mattera (σύγχρονη ζωγράφος)

Joanne Mattera (σύγχρονη ζωγράφος)

Sol LeWitt (1928 - 2007) - "Bands of Color in Four Directions"

Antonio Saporito (Σύγχρονος ζωγράφος) - "Parallel Lines"

Varvara Stepanova (1854 - 1958) - "Textile"

Όπυ Ζούνη (1941-2008) - "Φράχτης"

Τα βιβλία γράφουν...

Δύο ευθείες του ίδιου επιπέδου λέγονται παράλληλες, αν δεν έχουν κανένα κοινό σημείο, όσο κι αν προεκταθούν.

ΤΕΜΝΟΜΕΝΕΣ ΕΥΘΕΙΕΣ

Lyubov Popova (1889 - 1924) - "Space Force Construction" (1922)

Aleksandr Rodchenko (1891 - 1956) - "Non Objective Painting (Line)" (1919)

Τα βιβλία γράφουν...

Δύο ευθείες του ίδιου επιπέδου που έχουν ένα κοινό σημείο ονομάζονται τεμνόμενες. Το κοινό τους σημείο λέγεται σημείο τομής των δύο ευθειών.

ΚΑΘΕΤΕΣ ΕΥΘΕΙΕΣ

Sol LeWitt (1928 -2007) - "Centre"

Frank Stella (γεν. 1936) - "Hyena Stomp" (1962)

Piet Mondrian (1872 - 1944) - "Composition with Red, Yellow and Blue" (1942)

Slavomir Zombek (Σύγχρονος ζωγράφος) - "The Golden Ratio No 09"

Τα βιβλία γράφουν...

Δύο ευθείες είναι κάθετες, όταν οι γωνίες που σχηματίζουν αυτές τεμνόμενες,  είναι ορθές.

.*.〰.*.〰.*.〰.*.〰.*.〰.*.〰.*.

"Τα μάτια συλλαμβάνουν τους πιο λεπτούς μαθηματικούς λογισμούς παρά τις παραμορφώσεις της προοπτικής. Εκεί έγκειται ένα από τα μυστικά της μελαγχολικής ομορφιάς ορισμένων πινάκων".
Salvador Dali

.*.〰.*.〰.*.〰.*.〰.*.〰.*.〰.*.

Πηγές:

• Μαθηματικά Α' Γυμνασίου, Ινστιτούτο Τεχνολογίας Υπολογιστών και Εκδόσεων "Διόφαντος", 2016
• E.H. Gombrich, Το Χρονικό της Τέχνης, Μορφωτικό Ίδρυμα Εθνικής Τραπέζης, 1995
• Wassily Kandinsky, Σημείο-Γραμμή-Επίπεδο, Εκδόσεις Δωδώνη, 2013
• H.L.C Jaffe, Η ζωγραφική στον 20ό αιώνα, Εκδόσεις Νεφέλη, 1984
• wikipedia.org