Γρίφος: Ένας ξεχωριστός τετραψήφιος!

 

Τα Μαθηματικά στην Τέχνη: Η ταινία του Möbius

 

Αν είχαμε μια κενή σφαίρα με ένα μυρμήγκι στο εσωτερικό της, εύκολα θα αντιλαμβανόμασταν ότι η σφαίρα διαθέτει δύο διακεκριμένες όψεις. Ένα μυρμήγκι που περπατά στο εσωτερικό της σφαίρας δεν θα φτάσει ποτέ στην εξωτερική επιφάνεια. Επίσης, ένα μυρμήγκι που περπατά στο εξωτερικό της δεν πρόκειται να περάσει στο εσωτερικό.

Μια επίπεδη επιφάνεια που εκτείνεται ως το άπειρο προς όλες τις κατευθύνσεις διαθέτει, επίσης, δύο όψεις. Ένα μυρμήγκι που περπατά στη μία όψη δεν πρόκειται να βρεθεί ποτέ στην άλλη. Ακόμη και μια πεπερασμένη επίπεδη επιφάνεια, όπως μια σελίδα χαρτιού, θεωρείται δύο όψεων αν το μυρμήγκι δεν καταφέρει να "καβαλήσει" τις αιχμηρές ακμές του συνόρου της. Ομοίως, ένα κοίλο αντικείμενο τοροειδούς σχήματος σαν τον λουκουμά έχει δύο όψεις. 

Η πρώτη επιφάνεια μίας όψης που ανακαλύφθηκε και μελετήθηκε είναι η ταινία του Möbius.

Seth Bareiss (γεν. 1964) - "Forever Fish" (2005)

Τα βιβλία γράφουν... 

Η ταινία του Möbius είναι μια επιφάνεια με μία μόνο όψη και μόνο ένα σύνορο (συνοριακή γραμμή), ενώ δεν έχει προσανατολισμό.

M.C Escher (1898-1972) - "Möbius Strip I" (1961)

M.C Escher (1898-1972) - "Möbius Strip II - Red Ants" (1963)

Για να κατασκευάσει κανείς μια ταινία Möbius, αρκεί απλώς να ενώσει τα δύο άκρα μιας μακριάς ανοιχτής λωρίδας, αφού πρώτα περιστρέψει το ένα από αυτά κατά 180º ως προς το άλλο. Σε μια τέτοια επιφάνεια, ένα μυρμήγκι μπορεί να περπατήσει από ένα σημείο σε ένα άλλο, χωρίς ποτέ να διασχίσει μια ακμή.

M.C Escher (1898-1972) - "Möbius Horsemen" (1946)

Joachim Eriksen (σύγχρονος καλλιτέχνης) - "Möbius"

Joachim Eriksen (σύγχρονος καλλιτέχνης) - "Intermediate Dimension"

Προσπαθήστε να χρωματίσετε μια ταινία Möbius. Είναι αδύνατο να βάψετε τη μια πλευρά κόκκινη και την άλλη πράσινη, καθώς διαθέτει μια μόνο όψη. Αυτό σημαίνει ότι αν πάρουμε δύο οποιαδήποτε σημεία πάνω στην ταινία του Möbius, μπορούμε να σχεδιάσουμε μια συνεχή γραμμή, χωρίς ποτέ να διασχίσουμε ένα σύνορο (ακμή).  

Joachim Eriksen (σύγχρονος καλλιτέχνης) - "Über die Einfachheit der Dinge"

Η ταινία του Μέμπιους είναι μια μη προσανατολιζόμενη επιφάνεια. Παρατηρήστε ότι ο κάβουρας που κινείται πάνω σε αυτήν αντιστρέφεται (η μεγάλη του δαγκάνα από αριστερά πάει δεξιά) κάθε φορά που κάνει έναν πλήρη κύκλο. Αυτό δεν θα συνέβαινε αν ο κάβουρας κινούταν πάνω σε έναν τόρο.

Η ταινία του Möbius με τις ενδιαφέρουσες ιδιότητές της έχει αποτελέσει -και συνεχίζει να αποτελεί- έμπνευση για πολλούς καλλιτέχνες...

"Möbius" - Γλυπτό των Jennifer Macklem & Kip Jones 
που διακοσμεί το εξωτερικό της δημόσιας βιβλιοθήκης της Κελόουνα στον Καναδά.

"Möbius Ship" (2006) - Γλυπτό του Tim Hawkinson
που παριστάνει τον αέναο κύκλο της ταινίας του Möbius.
(Μουσείο Τέχνης της Ινδιανάπολης)

Joachim Eriksen (σύγχρονος καλλιτέχνης) - "Simplicity (Möbius band)", γλυπτό από αλάβαστρο

Η ανακάλυψή της αποδίδεται στους Γερμανούς μαθηματικούς August Ferdinand Möbius και Johann Benedict Listing το 19ο αιώνα, αν και μια δομή παρόμοια με την ταινία του Möbius φαίνεται στα ρωμαϊκά μωσαϊκά που χρονολογούνται γύρω στο 200-250 μ.Χ.  

Αρχαίο ρωμαϊκό μωσαϊκό, όπου απεικονίζεται μια δομή παρόμοια με την ταινία του Möbius  

Πηγές:

• Clifford Pickover (2006). Η Λωρίδα του Μέμπιους. Εκδόσεις Τραυλός, Αθήνα.
• DiscoverNewFields
• The Moebius Strip: Dr August Moebius's marvellous band in Mathematics, games, literature, art, technology and cosmology
• Wikipedia | Λωρίδα του Μέμπιους
• Zeichnungen von Joachim Eriksen

"Έρωτας και μαθηματικά"

 

«Σκεφτείτε να υποχρεωνόσασταν στο σχολείο να παρακολουθήσετε ένα μάθημα καλλιτεχνικών στο οποίο θα σας δίδασκαν μόνο πώς να βάψετε ένα φράχτη. Σκεφτείτε να μη σας έδειχναν ποτέ τους πίνακες του Λεονάρντο Ντα Βίντσι ή του Πικάσο. Θα σας βοηθούσε αυτό το μάθημα να εκτιμήσετε την τέχνη; Θα σας έκανε να θελήσετε να μάθετε περισσότερα;», αναρωτιέται ο κορυφαίος μαθηματικός και συγγραφέας Edward Frenkel στον πρόλογο του βιβλίου του, Έρωτας & Μαθηματικά, (Εκδ. Αλεξάνδρεια - Μετάφραση: Τεύκρος Μιχαηλίδης). Και διαπιστώνει: «Έτσι διδάσκονται τα μαθηματικά στο σχολείο, οπότε στα μάτια των περισσοτέρων από εμάς ισοδυναμούν με το να κάθεσαι και να παρακολουθείς τη μπογιά να στεγνώνει».

Δεν πρόκειται, όμως, για ένα βιβλίο που επιχειρεί, απλώς, να αποκαλύψει την κρυμμένη ομορφιά και το εύρος των μαθηματικών και να στηλιτεύσει τον συμβατικό τρόπο διδασκαλίας τους. Αλλά για ένα σύνθετο, συναρπαστικό ανάγνωσμα στο οποίο ο έρωτας του Frenkel για τα μαθηματικά - καθηγητής σήμερα στο Πανεπιστήμιο της Καλιφόρνιας στο Μπέρκλεϊ - συνυπάρχει με τις δυσκολίες που αντιμετώπισε στην προσπάθειά του να κατακτήσει τη γνώση, και με το πρόσφατο, φωτεινό εγχείρημά του. Αυτό τον καιρό εργάζεται σε ένα από τα σπουδαιότερα επιτεύγματα των τελευταίων πενήντα χρόνων: το Πρόγραμμα Λάνγκλαντς, μια μεγάλη Ενοποιημένη Θεωρία των Μαθηματικών.

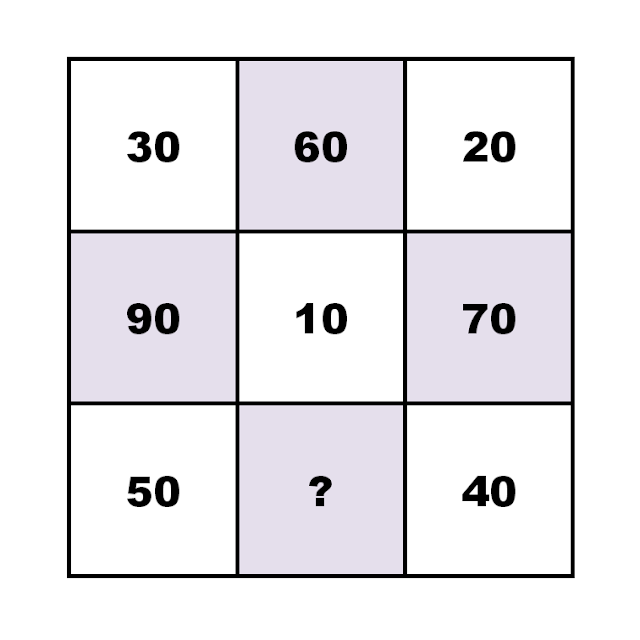
Γρίφος: Αριθμοί σε πίνακα

Βρείτε ποιος αριθμός πρέπει να αντικαταστήσει το ερωτηματικό. 

Πηγή: Διαγωνισμοί για την εισαγωγή στην Εθνική Σχολή Δημόσιας Διοίκησης και Αυτοδιοίκησης.

"Φίλιππος: Η Αποκάλυψη"

Η ζωή του Φίλιππου αλλάζει μετά την επιτυχία του σε μαθηματικό διαγωνισμό, που τον οδηγεί σε ένα ταξίδι στη σύγχρονη Αθήνα. Εκεί, αποκαλύπτεται η σύνδεσή του με τη χαμένη πόλη της Αρχαίας Ελίκης. Με μια μυστηριώδη φωτογραφική μηχανή που αποκαλύπτει το αρχαίο παρελθόν και με τη βοήθεια της αρχαιολόγου Δανάης, ο Φίλιππος πρέπει να σταματήσει τον γίγαντα Εγκέλαδο και τους συμμάχους του, Τιτάνες, που απειλούν να κυριεύσουν τον κόσμο κατά τη διάρκεια μιας σπάνιας πλανητικής ευθυγράμμισης... 

Οι Pan Stam (συγγραφή) και Jimmy D. Lupa (εικονογράφηση) έχουν δημιουργήσει μια συναρπαστική περιπέτεια φαντασίας γεμάτη θεούς και θρύλους, ενώ παράλληλα οι μαθηματικές αναφορές όπως ο αριθμός φ και ο μηχανισμός των Αντικυθήρων, δίνουν μια επιστημονική χροιά στην πλοκή. 

Αριθμοί Friedman

 

📖Ένας αριθμός Friedman είναι ένας θετικός ακέραιος που μπορεί να προκύψει χρησιμοποιώντας τα δικά του ψηφία, μαζί με ένα τουλάχιστον από τα σύμβολα +, -, ·, /, ^, (, ). 

• Τα ψηφία του χρησιμοποιούνται ακριβώς μία φορά το καθένα.
• Επιτρέπεται να συγκολληθούν δύο ή περισσότερα ψηφία.

Οι αριθμοί Friedman στο δεκαδικό σύστημα αρίθμησης, ξεκινώντας από τον μικρότερο, είναι:

\(25=5^2\)

\(121=11^2\)

\(125=5^{1+2}\)

\(126=6 \cdot 21\)

\(127=2^7-1\)

\(128=2^{8-1}\)

\(153=3 \cdot 51\)

\(216=6^{2+1}\)

\(289=(8+9)^2\)

\(343=(3+4)^3\)

\(347=7^3+4\)

\(625=5^{6-2}\)

\(688=8 \cdot 86\)

\(736=7+3^6\)

\(1022=2^{10}-2\)

\(1024=(4-2)^{10}\)

\(1206=6 \cdot 201\)

\(1255=5 \cdot 251\)

\(1260=6 \cdot 210 = 21 \cdot 60\)

\(1258=(1+2^8) \cdot 5\)

\(1296=6^{(9-1)/2}\)

\(1395=15 \cdot 93\)

\(1435=35 \cdot 41\)

\(1503=3 \cdot 501\)

\(1530=3 \cdot 510\)

\(1792=7 \cdot 2^{9-1}\)

\(1827=21 \cdot 87\)

\(2048=\frac{8^4}{2}+0=\frac{8^4}{2+0}\)

\(2187=(2+1^8)^7\)

\(2349=29 \cdot 3^4\)

 ...

📖Ένας πρώτος αριθμός Friedman είναι ένας αριθμός Friedman που επιπλέον είναι πρώτος.

Οι πρώτοι αριθμοί Friedman στο δεκαδικό σύστημα αρίθμησης είναι:

127, 347, 2503, 12101, 12107, 12109, 15629, 15641, 15661, 15667, 15679, 16381, 16447, 16759, 16879, 19739, 21943, 27653, 28547, 28559, 29527, 29531, 32771, 32783, 35933, 36457, 39313, 39343, 43691, 45361, 46619, 46633, 46643, 46649, 46663, 46691, 48751, 48757, 49277, 58921, 59051, 59053, 59263, 59273, 64513, 74353, 74897, 78163, 83357, ... 

 

📖Ένας αριθμός Friedman λέγεται ωραίος, όταν η μαθηματική έκφραση που τον συνθέτει, μπορεί να γραφεί έτσι, ώστε να περιέχει τα ψηφία με την ίδια σειρά που περιέχονται στον αριθμό.

Για παράδειγμα:

\(127=2^7-1=-1+2^7\)

\(343=(3+4)^3\)

Αν, μάλιστα, τυχαίνει να είναι και πρώτος, τότε λέγεται ωραίος πρώτος αριθμός Friedman. To 127 είναι ένας ωραίος πρώτος αριθμός Friedman.

Από την άλλη, το 121 και το 343 είναι παλινδρομικοί αριθμοί Friedman, αφού διαβάζονται το ίδιο είτε ευθέως είτε ανάποδα.

 

🧛🏻‍♂️Μια ειδική περίπτωση των αριθμών Friedman είναι οι βαμπιρικοί αριθμοί, όπως ο 1260 και ο 1395, τους οποίους είχαμε γνωρίσει σε παλιότερη ανάρτηση.

🖥️Μερικοί αριθμοί Friedman στο δυαδικό σύστημα αρίθμησης είναι: 11001, 11011, 111111, 1001111, 1010001, ...

(Αυτοί που σημειώνονται έντονα είναι ωραίοι αριθμοί Friedman, αλλά και παλινδρομικοί).

🌐Για περισσότερα, σας παραπέμπω:

Numbers Aplenty, Friedman Numbers 

Online Encyclopedia of Integer Sequences, Erich Friedman 

Γρίφος: Το άγγιγμα του Μίδα

 

Σε ένα σεντούκι θησαυρού υπάρχουν 4 χάλκινα νομίσματα, 4 ασημένια νομίσματα και 5 χρυσά νομίσματα. Όταν ο Μίδας αγγίζει τυχαία οποιοδήποτε νόμισμα οποιουδήποτε χρώματος, αυτό εξαφανίζεται μαγικά και αντικαθίσταται από δύο νέα νομίσματα που έχουν τα άλλα δύο χρώματα. Για παράδειγμα, αν ο Μίδας αγγίξει ένα ασημένιο νόμισμα, αυτό μεταμορφώνεται σε ένα χάλκινο νόμισμα και ένα χρυσό νόμισμα.

Μετά από δύο διαδοχικά τυχαία αγγίγματα του Μίδα, ποια είναι η πιθανότητα τα χρυσά νομίσματα να εξακολουθούν να είναι περισσότερα από οποιοδήποτε από τα άλλα δύο χρώματα;

Σημείωση: Ευχαριστώ τον φίλτατο Carlo De Grandi που μου έστειλε το γρίφο.

GIVEAWAY! Κερδίστε δύο βιβλία Μαθηματικών της Γ΄ Λυκείου! *ΕΛΗΞΕ*

Για τους μαθητές που έχουν μπει στην τελική ευθεία για τις Πανελλαδικές Εξετάσεις, αλλά και για τους καθηγητές τους, κυκλοφορεί το βιβλίο «ΜΑΘΗΜΑΤΙΚΑ Γ΄ ΛΥΚΕΙΟΥ… στην τελική ευθεία» από τον μαθηματικό και συγγραφέα Σπύρο Γιαννάκαρο και τις Εκδόσεις ΒΑΡΦΗΣ.

📚Στο περιεχόμενο του βιβλίου θα βρείτε:

• Συγκεντρωμένη τη θεωρία των Πανελλαδικών εξετάσεων

• 10 ολιγόλεπτα Τεστ ανά παράγραφο

• 15 θέματα θεωρίας σε όλη την ύλη

• Προτεινόμενες δραστηριότητες για την τάξη

• Μεθοδολογία σε βασικές κατηγορίες ασκήσεων, που συναντούμε συχνά σε θέματα των Πανελλαδικών εξετάσεων, με λυμένα παραδείγματα.

• Ασκήσεις εμπέδωσης

• Συνδυαστικά θέματα εφ’ όλης της ύλης

• Επαναληπτικά διαγωνίσματα

• Θέματα Πανελλαδικών εξετάσεων προηγουμένων ετών

• Αναλυτικές απαντήσεις των ασκήσεων εμπέδωσης, των συνδυαστικών θεμάτων (με παραπομπές στα αντίστοιχα κομμάτια της θεωρίας), των επαναληπτικών διαγωνισμάτων και των θεμάτων των Πανελλαδικών εξετάσεων.

 

🎁Δύο τυχεροί/τυχερές μπορούν από σήμερα να κερδίσουν από ένα αντίτυπο του βιβλίου «ΜΑΘΗΜΑΤΙΚΑ Γ΄ ΛΥΚΕΙΟΥ… στην τελική ευθεία», προσφορά του συγγραφέα, μέσα από το 4^ο giveaway που διοργανώνει το blog «εις το άπειρον»!

 

Για να πάρετε μέρος στην κλήρωση, πρέπει και αρκεί:

1.    Να είστε ακόλουθοι του blog «εις το άπειρον» (η εγγραφή γίνεται με χρήση gmail πατώντας πάνω στο μπλε κουμπάκι)

2.    Να αφήσετε ένα σχόλιο σ' αυτή την ανάρτηση, δηλώνοντας συμμετοχή στο giveaway και γράφοντας το e-mail σας

3.    Προσοχή: αν στο σχόλιο φαίνεστε ως ανώνυμοι, φροντίστε να γράψετε το όνομά σας  (δυστυχώς ανώνυμα σχόλια δεν μπορούν να ληφθούν υπόψη).

 

🎲Ο διαγωνισμός λήγει το Σάββατο 1 Φεβρουαρίου 2025 στις 23:59. Την Κυριακή 2 Φεβρουαρίου 2025, θα ανακοινωθούν στην παρούσα ανάρτηση οι 2 τυχεροί/τυχερές που θα αναδείξει η κλήρωση μέσω του randomname picker από το commentpicker.com και θα ειδοποιηθούν μέσω e-mail (στο e-mail που θα έχουν δηλώσει)! Τα δώρα θα σταλούν στους νικητές μόλις έχουμε τις διευθύνσεις τους. Αν κάποιος/α δεν επικοινωνήσει εντός μιας εβδομάδας, θα ξαναγίνει κλήρωση για να αναδειχθεί ο νικητής που θα τον αντικαταστήσει.

 

Καλή επιτυχία σε όλους!!!

 

=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=

EDIT 2/2/2025 - ΛΗΞΗ ΔΙΑΓΩΝΙΣΜΟΥ ΚΑΙ ΚΛΗΡΩΣΗ!

Σας ευχαριστούμε όλους και όλες όσοι/ες συμμετείχατε στο giveaway μας! Μέσω του random name picker από το commentpicker.com, πραγματοποιήθηκε η κλήρωση που ανέδειξε τους 2 τυχερούς!

Συγχαρητήρια στις δύο νικήτριες! Είμαι σίγουρη ότι το βιβλίο του Σ.Γιαννάκαρου θα αποδειχθεί πολύτιμος βοηθός στη δουλειά σας!

Αν η στατιστική ήταν... ζώο!

Γρίφος: Η ανταλλαγή

Κάποιος οδηγός χρειάζεται κέρματα, για να ρίξει στο μηχάνημα του parking. Ζητάει, λοιπόν, από τον περιπτερά να του ανταλλάξει ένα χαρτονόμισμα των 10€, με κέρματα του 1€ και των 50 λεπτών. Με πόσους τρόπους μπορεί να γίνει η ανταλλαγή, αν ο οδηγός θέλει οπωσδήποτε κέρματα και του 1€ και των 50 λεπτών;