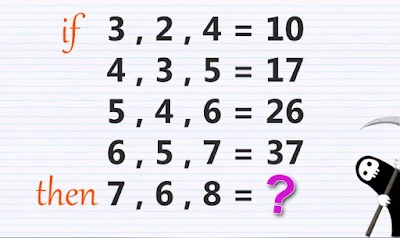Δευτέρα 28 Μαΐου 2018
Τετάρτη 23 Μαΐου 2018
Σύνθετο... φρουτο-κουίζ!
- Βρίσκουμε τον αριθμό στη θέση του λεμονιού
- Βρίσκουμε τον αριθμό στη θέση του μήλου
- Βρίσκουμε τον αριθμό στη θέση του πορτοκαλιού
- Βρίσκουμε τον αριθμό στη θέση του ερωτηματικού!
Αφήστε σχόλιο με τον αριθμό που βρήκατε... Η λύση θα δοθεί σύντομα!!!
Κυριακή 13 Μαΐου 2018
Τα Μαθηματικά στην Τέχνη: Υπερβολή
Μαθαίνουμε για την υπερβολή μέσα από έργα τέχνης...
 |
| Josh Hufford (Σύγχρονος καλλιτέχνης) - "Within The Emptiness: Hyperbola" |
 |
| Mary Rouncefield (Σύγχρονη καλλιτέχνιδα) - "Hyperbola" |
Τα βιβλία γράφουν...
Έστω Ε και Ε΄ δύο σημεία του επιπέδου. Ονομάζεται υπερβολή με εστίες τα σημεία Ε και Ε΄ ο γεωμετρικός τόπος C των σημείων του επιπέδου, των οποίων η απόλυτη τιμή της διαφοράς των αποστάσεων από τα Ε και Ε΄ είναι σταθερή και μικρότερη του Ε΄Ε. Η απόσταση Ε΄Ε ονομάζεται εστιακή απόσταση της υπερβολής.
 |
| Russell Kightley (Σύγχρονος καλλιτέχνης) - "Hyperbola" |
Τα βιβλία επίσης γράφουν...
Η υπερβολή μπορεί να προκύψει από την τομή ενός κώνου με ένα επίπεδο, γι' αυτό και είναι μία από τις κωνικές τομές.
.*.〰.*.〰.*.〰.*.〰.*.〰.*.〰.*.
"O πίνακας ζωγραφικής "Y=f(x)" δημιουργήθηκε με τη βοήθεια ενός μαθηματικού τύπου, συγκεκριμένα της συνάρτησης y=1/x. H καμπύλη που προκύπτει είναι μια υπερβολή. Η άλλη αρχή που χρησιμοποιήθηκε είναι αυτή της χρυσής τομής. Ήταν ενδιαφέρον να πειραματιστώ, θέλοντας να δείξω πώς μια μαθηματική έκφραση μπορεί επίσης να έχει αισθητική. Τα Μαθηματικά είναι παντού γύρω μας και μας πληροφορούν για την όλη ύπαρξη".
Slav Nedev
.*.〰.*.〰.*.〰.*.〰.*.〰.*.〰.*.
Πηγές:
- Μαθηματικά Θετικής και Τεχνολογικής Κατεύθυνσης Β' Γενικού Λυκείου, ΟΕΔΒ, 2003
- Θ. Κουφογιώργος, Μαθήματα Αναλυτικής Γεωμετρίας, Τυπογραφείο Πανεπιστημίου Ιωαννίνων, 2004
- E.H. Gombrich, Το Χρονικό της Τέχνης, Μορφωτικό Ίδρυμα Εθνικής Τραπέζης, 1995
- Wassily Kandinsky, Σημείο-Γραμμή-Επίπεδο, Εκδόσεις Δωδώνη, 2013
- Wassily Kandinsky, Για το πνευματικό στην Τέχνη, Εκδόσεις Νεφέλη, 1981
- H.L.C Jaffe, Η ζωγραφική στον 20ό αιώνα, Εκδόσεις Νεφέλη, 1984
- Deviant Art: Josh Hufford
- Fine Art America: Hyperbola
- Mary Rouncefield
- Saatchi Art: Slav Nedev
- wikipedia.org
Ετικέτες
αναλυτική γεωμετρία,
ατάκες κι αποφθέγματα,
καμπύλες στο επίπεδο,
κωνικές τομές,
μαθηματικά και τέχνη
Κυριακή 6 Μαΐου 2018
Τα Μαθηματικά στην Τέχνη: Παραβολή
Μαθαίνουμε για την παραβολή μέσα από έργα τέχνης...
 |
| Josh Hufford (Σύγχρονος καλλιτέχνης) - "This Holy Reality-Parabola" |
Τα βιβλία γράφουν...
Έστω μια ευθεία δ και ένα σημείο Ε εκτός της δ. Ονομάζεται παραβολή με εστία το σημείο Ε και διευθετούσα την ευθεία δ ο γεωμετρικός τόπος C των σημείων του επιπέδου τα οποία ισαπέχουν από την Ε και τη δ. Αν Α είναι η προβολή της εστίας Ε στη διευθετούσα δ, τότε το μέσο Κ του ΕΑ είναι προφανώς σημείο της παραβολής και λέγεται κορυφή της.
 |
| Russell Kightley (Σύγχρονος καλλιτέχνης) - "Parabola" |
Τα βιβλία επίσης γράφουν...
Η παραβολή μπορεί να προκύψει από την τομή ενός κώνου με ένα επίπεδο, γι' αυτό και είναι μία από τις κωνικές τομές.
Πηγές:
- Μαθηματικά Θετικής και Τεχνολογικής Κατεύθυνσης Β' Γενικού Λυκείου, ΟΕΔΒ, 2003
- Θ. Κουφογιώργος, Μαθήματα Αναλυτικής Γεωμετρίας, Τυπογραφείο Πανεπιστημίου Ιωαννίνων, 2004
- E.H. Gombrich, Το Χρονικό της Τέχνης, Μορφωτικό Ίδρυμα Εθνικής Τραπέζης, 1995
- Wassily Kandinsky, Σημείο-Γραμμή-Επίπεδο, Εκδόσεις Δωδώνη, 2013
- Wassily Kandinsky, Για το πνευματικό στην Τέχνη, Εκδόσεις Νεφέλη, 1981
- H.L.C Jaffe, Η ζωγραφική στον 20ό αιώνα, Εκδόσεις Νεφέλη, 1984
- Deviant Art: Josh Hufford
- Fine Art America: Jutta Maria Pusl
- Pixels: Russell Kightley
- Mary Rouncefield
- wikipedia.org
Κυριακή 22 Απριλίου 2018
Μετρώντας τη Γη: Ο μεγαλοφυής υπολογισμός του Ερατοσθένη
Η πρώτη φορά στην ιστορία κατά την
οποία έγινε πραγματική μέτρηση για τον υπολογισμό της περιμέτρου της Γης, ήταν
από τον Ερατοσθένη τον Κυρηναίο (276 πΧ – 194 πΧ), ο οποίος υπολόγισε με
εκπληκτική ακρίβεια την περίμετρο της Γης από... ένα πηγάδι. Για τη μέτρηση
αυτή ο Ερατοσθένης είχε γράψει ιδιαίτερη πραγματεία, όπως πληροφορούμαστε από
την «Διόπτρα» του Ήρωνος του Αλεξανδρέως, ο οποίος αναφερόμενος στο μέγεθος της
περιμέτρου της Γης σημειώνει: «Ερατοσθένης εν τω επιγραφομένω περί
αναμετρήσεως της Γης».
Ο
Ερατοσθένης γεννήθηκε στην ελληνική αποικία της Βόρειας Αφρικής, Κυρήνη και
ήταν φίλος με τον Αρχιμήδη. Λέγεται ότι είχε ζήσει στην Αθήνα για αρκετά
χρόνια, ώσπου έγινε βιβλιοθηκάριος στην περίφημη βιβλιοθήκη της Αλεξάνδρειας,
όπου και μελετούσε.
Πώς ένα
πηγάδι βοήθησε τον Ερατοσθένη να αποδείξει ότι η Γη είναι στρογγυλή...
Η άποψη ότι η
Γη ήταν σφαιρική ήταν αποδεκτή στην αρχαία Ελλάδα. Ο Ερατοσθένης ήταν εκείνος που απέδειξε μαθηματικά αυτή την
πεποίθηση και μάλιστα υπολόγισε με αξιοθαύμαστη ακρίβεια την ακτίνα και την
περίμετρο της σφαιρικής Γης.
Την εποχή που βρισκόταν στη βιβλιοθήκη, ο
Ερατοσθένης πληροφορήθηκε για ένα πολύ περίεργο πηγάδι, το οποίο
βρισκόταν κοντά στη
Συήνη (σημερινό Ασουάν της νότιας Αιγύπτου). Κάθε χρόνο, το μεσημέρι της 21ης Ιουνίου -
τη μέρα του θερινού ηλιοστασίου, δηλαδή τη μεγαλύτερη μέρα του έτους - ο Ήλιος
καθρεφτιζόταν ολόκληρος μέσα στο πηγάδι και το φώτιζε μέχρι τον πυθμένα του, χωρίς να δημιουργείται σκιά γύρω από
αυτό. Ο Ερατοσθένης συμπέρανε ότι για να συμβαίνει κάτι τέτοιο, τη
συγκεκριμένη μέρα ο Ήλιος έπρεπε να βρίσκεται ακριβώς κατακόρυφα πάνω από το πηγάδι.
Ο ήλιος όμως δεν συμπεριφερόταν το ίδιο και στα βόρεια της Αιγύπτου. Στην Αλεξάνδρεια, η οποία απέχει 800 χλμ από το Ασουάν, την ίδια εκείνη μέρα, ο
ήλιος δημιουργούσε μια μικρή σκιά σε μια ψηλή κολώνα.
Αυτό σήμαινε ότι οι δύο πόλεις σίγουρα δεν έβλεπαν τον ήλιο υπό την ίδια γωνία.
Ο Ερατοσθένης γνώριζε ήδη από προγενέστερες αστρολογικές μετρήσεις που διάβασε
στη βιβλιοθήκη ή από δικούς του υπολογισμούς, ότι η Συήνη και η Αλεξάνδρεια
ανήκαν στον ίδιο μεσημβρινό. Επομένως ο λόγος που ο Ήλιος δεν μπορούσε να
μεσουρανεί ταυτόχρονα στη Συήνη και στην Αλεξάνδρεια οφειλόταν στο ότι η Γη ήταν στρογγυλή και όχι επίπεδη.
Πώς ο Ερατοσθένης υπολόγισε την περίμετρο της Γης...
Το πείραμα του Ερατοσθένη βασίστηκε στη μέτρηση της γωνίας
υπό την οποία ο Ήλιος έστελνε τις ακτίνες του σε δύο διαφορετικές τοποθεσίες
(Αλεξάνδρεια και Συήνη), την ίδια χρονική στιγμή. Ο Ερατοσθένης πραγματοποίησε το πείραμα στις
21 Ιουνίου, την ημέρα του θερινού ηλιοστασίου, όταν η Γη παρουσιάζει τη μέγιστη
κλίση της ως προς τον Ήλιο. Αυτό σημαίνει ότι ο Ήλιος το μεσημέρι βρισκόταν
ακριβώς πάνω από τις δύο πόλεις.
Στο σχήμα
βλέπουμε παράλληλες ακτίνες να φτάνουν από τον Ήλιο στη Γη. Το μεσημέρι της 21ης
Ιουνίου, οι ηλιακές ακτίνες βυθίζονται στο πηγάδι της Συήνης, χωρίς να
δημιουργούν καμία σκιά, επομένως «κατευθύνονται» προς το κέντρο της Γης.
Την ίδια χρονική στιγμή στην Αλεξάνδρεια, μία ψηλή κολώνα (κάθετη στο έδαφος) σχηματίζει μια μικρή σκιά. Ο Ερατοσθένης μέτρησε το ύψος της κολώνας και το μήκος της σκιάς της. Έτσι δημιούργησε ένα ορθογώνιο τρίγωνο και, χρησιμοποιώντας την τριγωνομετρία, υπολόγισε τη γωνία που σχηματιζόταν ανάμεσα στην κολώνα και στις ακτίνες του Ήλιου. Το αποτέλεσμα ήταν ότι η γωνία ήταν φ = 7,2˚ , δηλαδή το 1/50 της περιφέρειας του κύκλου που είναι 360˚.
Εδώ έχει μεγάλη σημασία το ότι η γωνία φ ισούται με τη γωνία που σχηματίζεται ανάμεσα στις δύο ακτίνες που συνδέουν το κέντρο της Γης με την Αλεξάνδρεια και τη Συήνη αντίστοιχα (εντός εναλλάξ γωνίες).
Την ίδια χρονική στιγμή στην Αλεξάνδρεια, μία ψηλή κολώνα (κάθετη στο έδαφος) σχηματίζει μια μικρή σκιά. Ο Ερατοσθένης μέτρησε το ύψος της κολώνας και το μήκος της σκιάς της. Έτσι δημιούργησε ένα ορθογώνιο τρίγωνο και, χρησιμοποιώντας την τριγωνομετρία, υπολόγισε τη γωνία που σχηματιζόταν ανάμεσα στην κολώνα και στις ακτίνες του Ήλιου. Το αποτέλεσμα ήταν ότι η γωνία ήταν φ = 7,2˚ , δηλαδή το 1/50 της περιφέρειας του κύκλου που είναι 360˚.
Εδώ έχει μεγάλη σημασία το ότι η γωνία φ ισούται με τη γωνία που σχηματίζεται ανάμεσα στις δύο ακτίνες που συνδέουν το κέντρο της Γης με την Αλεξάνδρεια και τη Συήνη αντίστοιχα (εντός εναλλάξ γωνίες).
Στη συνέχεια, με την
βοήθεια του βασιλιά Πτολεμαίου, ο οποίος διέθεσε ένα είδος
οδομέτρου με γρανάζια, μέτρησε την απόσταση
των δύο πόλεων, που ήταν 5.040 στάδια. Στο πείραμα του, τα 5.040 στάδια αντιστοιχούσαν
στο 1/50 της περιφέρειας του κύκλου.
Τέλος, πολλαπλασίασε το 5.040 με το 100% του κύκλου, δηλαδή
το 50, και έτσι υπολόγισε την περίμετρο της Γης στα 252.000 στάδια, ή με τη
σύγχρονη μονάδα μέτρησης, 39.690 χιλιόμετρα. Ο υπολογισμός που έκανε ο
Ερατοσθένης 2.200 χρόνια πριν ήταν αρκετά ακριβής. Σήμερα η περίμετρος της
Γης υπολογίζεται σύμφωνα με δορυφορικές μετρήσεις σε 40.048 χιλιόμετρα, άρα
στην ουσία έπεσε έξω μόλις 358 χιλιόμετρα!
Πηγες:
Τζόνι Μπολ, Μαθημαγικά, Εκδόσεις Polaris, 2011
wikipedia.org
Δευτέρα 9 Απριλίου 2018
Τα Μαθηματικά στην Τέχνη: Έλλειψη
Μαθαίνουμε για την έλλειψη μέσα από έργα τέχνης.
 |
| Kazimir Malevich (1879 - 1935) - "Black Cross on Red Oval" |
 |
| Ellsworth Kelly (1923 - 2015) - "Red/Blue" (1964) |
 |
| Ellsworth Kelly (1923 - 2015) - Blue and Yellow and Red-Orange |
 |
| Josh Hufford (Σύγχρονος καλλιτέχνης) - "Tedious Path-Ellipse" |
 |
| Mary Rouncefield (Σύγχρονη καλλιτέχνιδα) - "Ellipse" |
 |
| "Oval Hanging Construction", κρεμαστό γλυπτό του Alex Rodchenko (1921) |
Τα βιβλία γράφουν...
Έλλειψη λέμε το σύνολο των σημείων του επιπέδου, των οποίων το άθροισμα των αποστάσεων από δύο σταθερά σημεία (εστίες της έλλειψης) είναι σταθερό και μεγαλύτερο από την απόσταση μεταξύ των εστιών.
 |
| Russell Kightley (Σύγχρονος καλλιτέχνης) - "Conic Sections: Ellipse" |
Τα βιβλία επίσης γράφουν...
Η έλλειψη μπορεί να προκύψει από την τομή ενός κώνου με ένα επίπεδο, γι' αυτό και είναι μία από τις κωνικές τομές.
.*.〰.*.〰.*.〰.*.〰.*.〰.*.〰.*.
"Ο θεωρητικός μαθηματικός, όπως ο μουσικός, είναι ένας ελεύθερος δημιουργός ενός κόσμου διατεταγμένης ομορφιάς".
Bertrand Russel (1872 - 1970)
.*.〰.*.〰.*.〰.*.〰.*.〰.*.〰.*.
Πηγές:
- Μαθηματικά Θετικής και Τεχνολογικής Κατεύθυνσης Β' Γενικού Λυκείου, ΟΕΔΒ, 2003
- Θ. Κουφογιώργος, Μαθήματα Αναλυτικής Γεωμετρίας, Τυπογραφείο Πανεπιστημίου Ιωαννίνων, 2004.
- E.H. Gombrich, Το Χρονικό της Τέχνης, Μορφωτικό Ίδρυμα Εθνικής Τραπέζης, 1995
- Wassily Kandinsky, Σημείο-Γραμμή-Επίπεδο, Εκδόσεις Δωδώνη, 2013
- Wassily Kandinsky, Για το πνευματικό στην Τέχνη, Εκδόσεις Νεφέλη, 1981
- H.L.C Jaffe, Η ζωγραφική στον 20ό αιώνα, Εκδόσεις Νεφέλη, 1984
- Deviant Art: Josh Hufford
- Mary Rouncefield
- Pixels: Russell Kightley
- wikipedia.org
Ετικέτες
αναλυτική γεωμετρία,
ατάκες κι αποφθέγματα,
καμπύλες στο επίπεδο,
κωνικές τομές,
μαθηματικά και τέχνη
Σάββατο 31 Μαρτίου 2018
Τα τελευταία λόγια μεγάλων μαθηματικών!
→Αρχιμήδης: «Εύρηκα... αλλά άρπαξα ένα κρύωμα!»
→Πυθαγόρας: «Μας κάρφωσε ο Ίππασος !!!»
→Ευκλείδης: «Το 5ο αίτημα
δεν μου πολυαρέσει!!!»
→Ερατοσθένης: «Είδε
κανείς το κόσκινό μου;»
→Ζήνων: «Είδες η
χελώνα;»
→Διόφαντος: «Η ηλικία μου, ένα αίνιγμα…»
→Νεύτωνας : «Δεν
ξαναπερνάω κάτω από μηλιά».
→Γαλιλαίος: «Και
όμως, γυρίζει…»
→Καρτέσιος: «Σε λίγο θα πάψω να σκέπτομαι και να υπάρχω!!»
→Τζιρόλαμο Καρντάνο: «Αυτός ο κερατάς ο Ταρτάλια μου
έκλεψε την απόδειξη!»
→Πιερ Ντε Φερμά: «Έχω βρει μια πολύ ωραία απόδειξη
αλλά δεν
προλαβαίνω να την γράψω, μου χτυπάνε το κουδούνι...»
→Γκαλουά: «Έπρεπε να φορέσω αλεξίσφαιρο…»
→Λάιμπνιτς: «Υπήρξα πολύ αγαπητός!!!» (μόνο τρία άτομα συνόδευαν την σορό
του).
→Μπερνούλι: «Θα ξαναγυρίσω αλλαγμένος».
→Λέοναρντ Όιλερ: «Δεν βλέπω τίποτα».
→Καντόρ : «Τελικά
ο Σαίξπηρ ήταν ο Φράνσις Μπέικον;»
→Πασκάλ: «Τα τρίγωνα μου μέσα!!»
→Φιμπονάτσι: «Ποιος άφησε ελεύθερα τα κουνέλια;»
→Ραμανουτζάν : «Εγώ δεν έκανα τίποτα... Όλα τα έκανε
η Ναμαγκίρι».
→Χίλμπερτ: «Τώρα ποιος θα λύσει τα προβλήματα μου;»
→Μπέρτραντ Ράσελ: «Πάλι αυτός ο κουρέας είναι
ακούρευτος!!»
→Πωλ Έρντος: «Πάω τώρα να κρυφοκοιτάξω το βιβλίο...»
→Γκόλντμπαχ: «Το πολύ σε ένα χρόνο θα έχουν αποδείξει
την εικασία μου».
→Τζορτζ Μπουλ: «Λογικά
θα πεθάνω!»
→Αύγουστος Φερδινάνδος Μέμπιους: «Είδε κανείς την λωρίδα μου;»
→Αύγουστος Ντε Μόργκαν: «Εκείνος ο χάρτης, πόσα χρώματα;»
→Αβραάμ Ντε Μουάβρ: «Έχω αϋπνίες..»
→Γκέντελ: «Πλήρης...»
→Ουίλιαμ Σάνκς: «Εγώ δεν λαθεύω ποτέ και αυτό είναι το
μοναδικό μου λάθος».
→Τ.Χάρντι: « Όλα
είναι θέμα spin».
→Αϊνστάιν: «Σχετικά
είναι όλα...»
Δευτέρα 5 Μαρτίου 2018
Τα Μαθηματικά στην Τέχνη: Κύκλος
Θα μάθουμε τον κύκλο μέσα από πίνακες ζωγραφικής και ψηφιακά σχέδια...
 |
| Wassily Kandinsky (1866 - 1944) - Squares with Concentric Circles (1913) |
 |
| Wassily Kandinsky (1866 - 1944) - Circles within a circle (1923) |
 |
| Wassily Kandinsky (1866 - 1944) - Several Circles (1926) |
 |
| Donald K. Sultan (γεν. 1951) - Double Dominos |
 |
| Sharon Horvath (Σύγχρονη ζωγράφος) - Moons (2016) |
 |
| Laszlo Moholy-Nagy (1895 - 1946) |
 |
| Kazuya Akimoto (Σύγχρονος ζωγράφος) - "Colorful Planets" |
 |
| Lazar Markovich Lissitzky (El Lissitzky) (1890 - 1941) |
 |
| Lazar Markovich Lissitzky (El Lissitzky) (1890 - 1941) |
 |
| Jasper Johns (γεν. 1930) - "Target with Four Faces" (1955) |
 |
| Paul Klee (1879 - 1940) - Senecio (1922) |
 |
Florin Constantinescu (Σύγχρονος καλλιτέχνης) - Uncertainties (2016)
James Pinkerton (γεν. 1958) - Blue Plate Special |
 |
| Julie Gross (Σύγχρονη ζωγράφος) - "Blue Inversion" (2004) |
 |
| Mairi Walker (Σύγχρονη καλλιτέχνιδα και μαθηματικός) (2013) |
Τα βιβλία γράφουν...
Κύκλο λέμε το επίπεδο σχήμα, κάθε σημείο του οποίου απέχει ίση απόσταση (ακτίνα) από ένα σταθερό σημείο
(κέντρο του κύκλου).
Τα βιβλία επίσης γράφουν...
Κύκλος (Ο,ρ) λέγεται ο γεωμετρικός τόπος των σημείων Μ του επιπέδου για τα οποία ισχύει:
ΟΜ = ρ.
Τα βιβλία γράφουν...
Ο κύκλος μπορεί να προκύψει από την τομή ενός κώνου με ένα επίπεδο, γι' αυτό και είναι μία από τις κωνικές τομές.
Ο κύκλος μπορεί να προκύψει από την τομή ενός κώνου με ένα επίπεδο, γι' αυτό και είναι μία από τις κωνικές τομές.
Πηγές:
- Μαθηματικά Θετικής και Τεχνολογικής Κατεύθυνσης Β' Γενικού Λυκείου, ΟΕΔΒ, 2003
- Ευκλείδεια Γεωμετρία Α' και Β' Γενικού Λυκείου, Ινστιτούτο Τεχνολογίας Υπολογιστών και Εκδόσεων "Διόφαντος", 2015
- Θ. Κουφογιώργος, Μαθήματα Αναλυτικής Γεωμετρίας, Τυπογραφείο Πανεπιστημίου Ιωαννίνων, 2004.
- E.H. Gombrich, Το Χρονικό της Τέχνης, Μορφωτικό Ίδρυμα Εθνικής Τραπέζης, 1995
- Wassily Kandinsky, Σημείο-Γραμμή-Επίπεδο, Εκδόσεις Δωδώνη, 2013
- Wassily Kandinsky, Για το πνευματικό στην Τέχνη, Εκδόσεις Νεφέλη, 1981
- H.L.C Jaffe, Η ζωγραφική στον 20ό αιώνα, Εκδόσεις Νεφέλη, 1984
- Pixels: Russell Kightley
- wikipedia.org
Παρασκευή 23 Φεβρουαρίου 2018
Μαθηματικές... προκλήσεις!
Για σήμερα συγκέντρωσα μερικούς διασκεδαστικούς γρίφους που βρήκα στο διαδίκτυο... Πραγματικά, είναι εθισμός! Εσείς τι λέτε?
#1
#2
#3
#4
#5
#6
Update: Θα βρείτε τις απαντήσεις εδώ...
Τετάρτη 14 Φεβρουαρίου 2018
Εγγραφή σε:
Σχόλια (Atom)